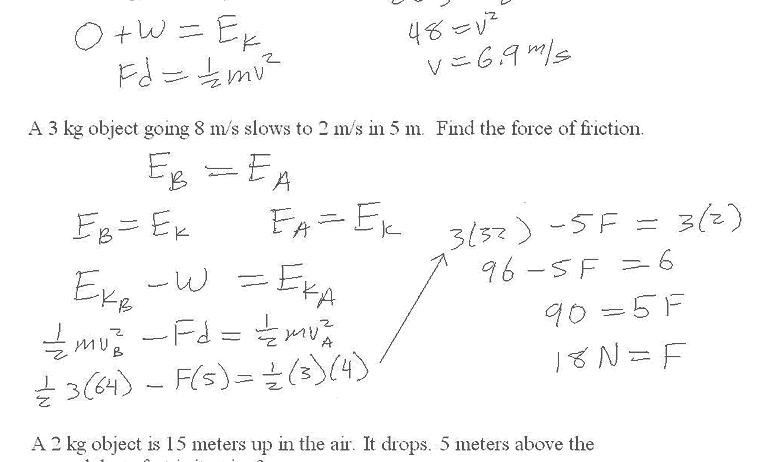Conservation of mechanical energy is akin to observing the dance of the pendulum, where potential and kinetic energies weave a seamless tapestry of motion. This intrinsic principle of physics not only defines how objects come to life but also illustrates the beauty of energy transformation. Step into the realm of mechanics, and let us unravel the intricacies of solving conservation of mechanical energy problems through a structured methodology.
Understanding Mechanical Energy
Mechanical energy is the sum of kinetic energy (KE) and potential energy (PE) within a system. Kinetic energy, defined as the energy of an object in motion, is described mathematically as KE = ½ mv², where m is mass and v is velocity. On the other hand, gravitational potential energy is the stored energy of an object due to its height in a gravitational field, given by the equation PE = mgh, with g representing the acceleration due to gravity and h the height above a reference point.
According to the principle of conservation of energy, in an isolated system, the total mechanical energy remains constant as long as only conservative forces are doing work. This forms the bedrock of our exploration into problem-solving.
Step 1: Identify the System and Relevant Forces
Every problem begins with defining the system under consideration. This could range from a pendulum swinging back and forth to a roller coaster barreling down a track. Isolate the forces acting on the object. Are there any non-conservative forces at play, such as friction or air resistance? Understanding this helps discern whether total mechanical energy is conserved.
Step 2: Determine the Initial and Final States
Visualizing the motion as the proverbial butterfly flits from flower to flower, detailing the initial and final states of the object involved is crucial. What are the heights, velocities, and forces acting at these two points? Clearly outline the initial state (starting position) and the final state (ending position) of the object. For example, if you observe a ball rolling down a hill, take note of its initial height and the velocity it attains at the bottom.
Step 3: Write the Conservation of Mechanical Energy Equation
The beauty of conservation lies in equating the initial and final mechanical energy. Express this mathematically: PE_initial + KE_initial = PE_final + KE_final. This equation acts as a bridge, seamlessly connecting the two disparate states of the system.
For instance, if we’re considering a ball dropped from a height, the initial kinetic energy is zero (since it’s at rest), leading us to PE_initial = mgh and KE_final = ½ mv² once the ball reaches the ground.
Step 4: Solve for Unknown Variables
With the equation established, it is now time to bridge the gap between what is known and what is unknown. Do you need to find velocity, height, or maybe the mass? Rearranging the equation to solve for these variables can feel like unraveling a tightly knotted thread. For the earlier example, with the ball’s height defined, momentum can be determined at the point of impact with Earth:
mgh = ½ mv²
By eliminating mass (as it appears on both sides), you can isolate v:
gh = ½ v² ⇒ v = √(2gh)
Step 5: Consider Complex Scenarios
As with any complex ballet, various elements can complicate the dance of mechanical energy. If additional forces come into play, such as friction, you may find that kinetic energy is not conserved. This is where the concept of non-conservative forces emerges. The work done against such forces must be accounted for, typically expressed in energy terms. For instance, if frictional forces dissipate some energy as heat, this energy loss must be added to your equation as:
PE_initial + KE_initial - Work_done_by_friction = PE_final + KE_final
Step 6: Verify Your Results
Just as a maestro scrutinizes each member of the orchestra, checking your solutions is paramount. Double-check the calculations and re-assess whether the answers align with physical realities. Does the velocity seem plausible? Is potential energy at a maximum when the object reaches its apex? Ensure that your conclusions stand firm against the laws of physics.
Step 7: Extend the Application
The allure of conservation of mechanical energy transcends simple problem-solving. Extend your grasp beyond textbook problems into the grand theater of real-world applications—roller coasters, pendulum clocks, and even planetary motion. Understanding these principles fosters a deeper appreciation of nature’s means of maintaining balance and order.
In conclusion, mastering the art of solving conservation of mechanical energy problems is like learning the steps to a timeless waltz. It requires understanding, practice, and a harmonic interplay of potential and kinetic energy. As you embrace these concepts, remember that energy never ceases; it merely transforms, creating an everlasting cycle of motion that echoes through the universe. Allow the dance of energy to unfold before your eyes, enriching both your mind and spirit with its captivating rhythms.