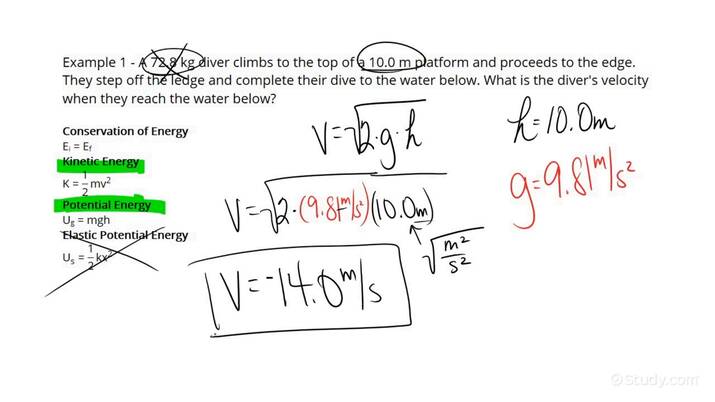Physics often reveals profound truths about our universe, illuminating the underlying principles that govern motion and energy. One such principle is the Conservation of Energy Theorem. This theorem posits that energy cannot be created or destroyed; it can only be transformed from one form to another. A compelling application of this theorem is in determining the final velocity of an object in motion, which is a common problem in physics. Understanding how to find final velocity using conservation of energy is a fundamental skill that not only enriches our grasp of physics but serves as a gateway into the intricate dance of forces that characterize our world.
At its essence, the Conservation of Energy Theorem asserts that the total mechanical energy—comprising kinetic and potential energy—of an isolated system remains constant. When an object is in motion, it possesses kinetic energy, which depends on its mass and velocity. Meanwhile, potential energy is often influenced by the object’s position within a gravitational field. Therefore, to compute the final velocity of an object, a clear understanding of both forms of energy is required.
Consider a simple scenario: a ball is thrown vertically upward. As the ball ascends, its velocity diminishes until it momentarily reaches a peak height, at which point its kinetic energy is at a minimum, while its potential energy is at a maximum. Consequently, when the ball returns to its original position, it reclaimes kinetic energy equivalent to what it had when it was first released. This exemplifies the essence of energy conversion—an exchange between kinetic and potential energy.
To illustrate how to apply this principle practically, we can derive an equation for determining the final velocity of an object. The total mechanical energy at the initial position equals the total mechanical energy at the final position. Mathematically, this is expressed as:
Initial Kinetic Energy + Initial Potential Energy = Final Kinetic Energy + Final Potential Energy
This equation can be rewritten as:
( frac{1}{2} mv_i^2 + mgh_i = frac{1}{2} mv_f^2 + mgh_f )
Where:
- m is the mass of the object.
- v_i is the initial velocity.
- h_i is the initial height.
- v_f is the final velocity.
- h_f is the final height.
In this equation, when dealing with problems where there is no change in height (i.e., when h_i = h_f), the potential energy terms cancel out, simplifying the equation to:
( frac{1}{2} mv_i^2 = frac{1}{2} mv_f^2 )
From this, one can manipulate the equation to find the final velocity:
v_f = v_i
This scenario predominantly deals with horizontal motion, and while it may appear straightforward, the applications of energy conservation principles extend far beyond simple cases. In more complex situations, such as oblique launches or free-fall dynamics, potential and kinetic energies fluctuate dynamically as the object traverses its path.
Consider a projectile launched at an angle. As it ascends, its speed decreases until it reaches its apex. At this point, its velocity has diminished significantly. Using conservation of energy principles, one can evaluate the behavior and final velocity of the projectile during both its ascent and descent. The mathematical framework becomes slightly more intricate, necessitating trigonometric functions to resolve the velocity components acting along both the x and y axes.
This leads us to a crucial insight: energy conservation is not an isolated phenomenon but interacts with various forces, including air resistance and friction. Although physics ideally simplifies situations, real-world applications rarely occur in vacuum. Thus, it’s essential to consider these dissipative forces, which absorb energy, leading to a reduction in mechanical energy present within the system.
Such considerations invite fascinating questions about energy efficiency, sustainability, and the environment. For instance, understanding how energy transforms within vehicles provides significant insights into fuel consumption and emissions, driving home the importance of conserving energy in our day-to-day applications. Similarly, analyzing the energy transfer methods in various natural systems elucidates nature’s inefficiencies and can serve as inspiration for more sustainable practices.
Furthermore, when delving into the realm of renewable energy, the principles of energy conservation are paramount. As we strive to enhance the efficiency of solar panels, wind turbines, and other renewable energy technology, a nuanced comprehension of energy transformations enables us to innovate more responsible solutions to contemporary challenges.
Energy conservation is not merely an academic exercise; rather, it serves as a lens through which to understand broader ecological and societal dynamics. The quest to optimize energy systems and practices fundamentally shapes our choices and ultimately impacts the climate and environment. Each calculation of final velocity, every application of the conservation of energy theorem, contributes to a deeper understanding of the interconnected world we inhabit.
In conclusion, mastering the concept of final velocity through conservation of energy is not merely an intellectual endeavor; it is a fundamental building block that connects various realms of physics and environmental consciousness. Understanding these principles equips individuals with the tools necessary to confront the challenges of energy consumption, sustainability, and climate change, thereby fostering a more informed and responsible society.