The universe operates on intricate laws that govern the constancy of energy, reflected beautifully in the concept of gravitational force. Just as the sun draws the planets into a harmonious dance, gravitational force is the invisible thread weaving the fabric of matter together. Understanding how to find gravitational force in the conservation of energy equation is akin to deciphering the harmony within this cosmic ballet. In the realm of physics, gravitational force (F) not only epitomizes a fundamental interaction but also serves as a pivotal component in energy conservation contexts.
At the core of this inquiry lies Newton’s Law of Universal Gravitation. This principle posits that every particle of matter in the universe attracts every other particle with a force that is directly proportional to the product of their masses and inversely proportional to the square of the distance between their centers. Mathematically, this can be expressed as:
F = G * (m1 * m2) / r²
Where:
- F is the gravitational force between the objects,
- G is the gravitational constant (approximately 6.674 × 10^-11 N(m/kg)²),
- m1 and m2 are the masses of the two objects, and
- r is the distance between the centers of the two masses.
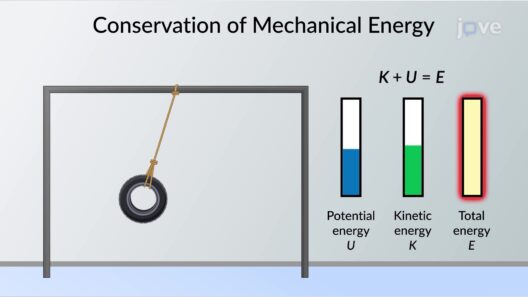
In the tapestry of energy conservation, gravitational force plays a vital role. Conservation of energy states that within a closed system, energy cannot be created or destroyed but can only transform from one form to another. This tenet holds true when considering gravitational potential energy (GPE), which is the energy stored in an object as a result of its vertical position or height. The equation for gravitational potential energy is succinctly represented as:
GPE = m * g * h
Where:
- m is the mass of the object,
- g is the acceleration due to gravity (approximately 9.81 m/s² on Earth), and
- h is the height above a reference point.
Incorporating gravitational force into the framework of energy conservation facilitates a seamless transition between states of potential and kinetic energy. As an object descends from a height, the gravitational potential energy morphs into kinetic energy, which is the energy of motion described as:
KE = 1/2 * m * v²
Here, v denotes the velocity of the object. This metamorphosis from potential to kinetic energy is an embodiment of energy conservation, where the potential energy lost is accounted for by an equivalent increase in kinetic energy.
To understand the dynamics involved in this conversion, consider a scenario where an object is released from a certain height. As the object descends, it experiences an acceleration of g, the acceleration due to gravity. This acceleration acts as the gravitational force, continuously impelling the object downward, demonstrating how the force influences energy dynamics. The interplay between gravitational force and energy conservation can be conceptualized as the rhythmic heartbeat of the universe—an eternal cycle that perpetuates movement and stability.
The gravitational force also serves as a crucial determinant in understanding orbits and celestial phenomena. Consider the Earth and the moon; their mutual gravitational attraction governs their orbit around a common center of mass, known as the barycenter. Herein lies a fascinating metaphor: consider the Earth and moon akin to dancers entwined in a gravitational waltz, perfunctorily adhering to the cadence dictated by their masses and the distance between them. The gravitational force, ever-present yet unseen, binds them together while allowing for a magnificent display of energy transformation as they orbit through space.
In practical applications, calculating gravitational force in the context of the conservation of energy equation can be instrumental in various fields such as engineering, astrophysics, and environmental science. Understanding the gravitational interactions allows for the design of structures that can withstand forces without yielding or collapsing. Moreover, comprehending these principles enables us to harness wind and solar energy by appreciating the gravitational interplay at work.
When conducting experiments to find the gravitational force using the conservation of energy, one method involves measuring the drop of an object. By calculating the height from which it falls and measuring its velocity just before impact, you can ascertain the kinetic energy at that moment. The gravitational potential energy possessed at the initial height will equal the kinetic energy just prior to impact, given negligible air resistance.
In summary, elucidating the gravitational force within the conservation of energy equation transcends mere calculations; it invites us into a profound comprehension of the universe’s interconnectedness. The gravitational force, akin to an unseen maestro, orchestrates not just the movement of celestial bodies but the very essence of energy transformation. As we delve into the minutiae of these cosmic phenomena, we begin to appreciate the elegance and precision with which nature constructs its operatic narrative, urging us to respect and protect the delicate balance that sustains life on our planet.