The concept of kinetic energy, akin to an invisible current flowing through the essence of motion, embodies the transformative power of moving bodies. To comprehend whether kinetic energy is conserved in a given system is to delve into the nuances of interactions and transformations. This exploration invokes an intellectual adventure, much like navigating a winding river where the waters are both delicate and forceful. Here, we shall elucidate the methodologies capable of deciphering the conservation of kinetic energy, interwoven with illustrative metaphors and critical insights into fundamental principles.
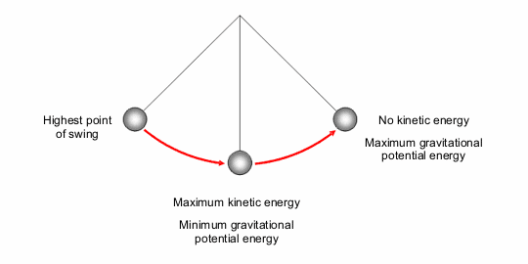
In the realm of physics, the principle of conservation states that in a closed system devoid of external forces, the total mechanical energy remains constant. This encompasses both kinetic energy—energy attributable to motion—and potential energy—the energy stored due to position. Understanding this equilibrium is essential for discerning instances where kinetic energy conservation holds true, creating a tapestry of relationships that govern dynamics.
First, consider the pivotal role of collisions. Collisions are the dramatic points in our narrative, acting as the climax of our kinetic energy tale. Just as a thunderous clap signals the onset of a storm, collisions alert us to shifts in energy states. There are two primary categories of collisions: elastic and inelastic. In elastic collisions, kinetic energy remains conserved, much like a perfectly smooth dance where partners exchange energy without loss. Observing the velocities of the colliding objects before and after impact can reveal whether energy is conserved. If the sum of kinetic energy before the collision matches the sum after, one can affirm the harmony of elastic exchange.
In contrast, inelastic collisions resemble a tempest where dancers fall out of sync, losing energy to other forms such as heat and sound. The hallmark of inelastic collisions is that the kinetic energy will not be conserved. Here, the interplay of energy degrades into unobserved realms, illustrating how energy morphs rather than disappears. To evaluate a scenario involving inelastic collisions, a quantitative analysis of kinetic energy pre- and post-collision is essential. If the numbers correlate, we find ourselves in the embrace of an elastic event; if they diverge, the shadows of inelasticity loom.
Furthermore, another significant indicator of kinetic energy conservation is the concept of closed systems. Imagine a system as a hermetically sealed vessel, where nothing enters nor escapes. In essence, a closed system creates a sanctuary for energy conservation. Surrounding forces, be they friction or air resistance, act as eroding agents against the conservation principle. Hence, when scrutinizing a system, one must ensure that it remains insulated from external influences. Only in this cocoon can one fully appreciate the constancy of total energy.
The consideration of external forces constitutes a vital variable within our equation. Gravity, friction, and other forces may add or subtract from the overall energy landscape, akin to a restless artist making uninvited strokes on a painting. Determining whether kinetic energy is conserved involves meticulous observation of these external inputs. If such forces are negligible, the conservation of kinetic energy can generally be assumed, crafting a clearer picture of the prevailing dynamics.
Mathematical rigor also provides an essential lens through which to analyze kinetic energy. Kinetic energy is quantitatively defined as KE = ½ mv², where ‘m’ denotes mass and ‘v’ denotes velocity. Through careful assessment of these variables, one can ascertain changes in kinetic energy across different states of motion. Evaluating mass and velocity before and after a dynamic event offers a comparative framework, a scientific detective examining clues to unscramble the mysteries of energy flow.
Moreover, the conservation of momentum, closely tied with the fate of kinetic energy, offers another dimension to our inquiry. The law of conservation of momentum dictates that the total momentum of a closed system remains constant in the absence of external forces. This principle acts like an anchor—a steadfast entity that stabilizes our understanding of motion. By examining momentum before and after an event, one can infer possible conservation scenarios for kinetic energy. Momentum (p) is defined as p = mv; observing how momentum changes can illuminate the intricate dance of kinetic energy through interactions.
In applying these principles, experimental models abound, paving the way for practical understanding. Simple setups using custom-built tracks or pendulums can serve as a microcosm for examining kinetic energy. Observing these physical systems allows one to visualize energy transformation, encapsulating the transition between potential and kinetic forms. Engaging with such demonstrable principles substantiates the theoretical underpinnings, tying knowledge to experience.
Ultimately, understanding whether kinetic energy is conserved is not merely an academic exercise but rather a reflection of the intricate interplay of forces and motions. Such inquiry invites a deeper appreciation of the world around us, akin to peering through a microscope and observing the intricate, interconnected fabric of energy transactions. It fosters a sense of responsibility, encouraging informed perspectives on energy use, efficiency, and sustainable practices, vital for a world striving for resilience in the face of climate challenges.
In conclusion, navigating the intricacies of kinetic energy conservation requires a multifaceted approach. By examining collisions, understanding the implications of external forces, evaluating mathematical formulations, and harnessing the law of conservation of momentum, one can cultivate a profound comprehension of how kinetic energy behaves in various conditions. Just as the currents of a river persist through the landscape, so too does the concept of kinetic energy flow, inviting inquiry and exploration in the magnificent theater of physics.