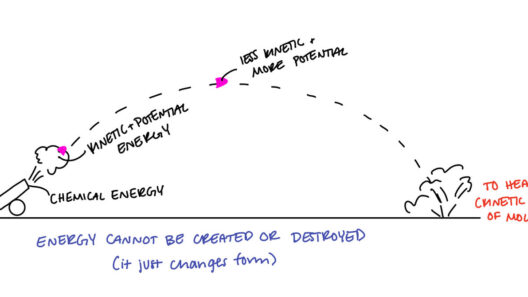
In the realm of physics, the conservation of energy theorem serves as a cornerstone for understanding how energy transformations influence motion. It posits that the total energy in a closed system remains constant over time. This principle is particularly pivotal in determining the initial velocity of objects in motion, a concept that not only captivates the imagination but also fosters a profound comprehension of various physical phenomena. Here, we delve into the methodology of finding initial velocity using the conservation of energy, elucidating the fundamental concepts, implications, and applications.
1. Understanding Energy Types
To embark on our exploration, we must first comprehend the various forms of energy present in a system. Primarily, we distinguish between kinetic energy and potential energy. Kinetic energy (K) is the energy possessed by an object due to its motion, defined mathematically as K = 1/2 mv², where m is mass and v is velocity. Conversely, potential energy (U) is stored energy based on an object’s position. Gravitational potential energy, for example, is expressed as U = mgh, where g is acceleration due to gravity and h is height above a reference point.
2. The Principle of Conservation of Energy
The conservation of energy states that within a closed system, the total mechanical energy (the sum of kinetic and potential energy) remains constant. This principle can be articulated mathematically in the following manner:
K_initial + U_initial = K_final + U_final
When applied judiciously, this equation facilitates the determination of unknown variables, including initial velocity. It is essential to recognize that energy can transition between kinetic and potential forms; for instance, as an object descends, its potential energy converts into kinetic energy, thereby increasing its velocity.
3. Setting Up the Problem
Consider a scenario where an object is projected from a certain height. Here, we aim to ascertain its initial velocity as it reaches the ground. To solve this, we must gather necessary parameters: the object’s mass (m), the height from which it is dropped (h), and the acceleration due to gravity (g, approximately 9.81 m/s² on Earth).
Initially, at the height h, the object possesses maximum potential energy and negligible kinetic energy (assuming it starts from rest). Therefore, we can express this energy state as:
U_initial = mgh
K_initial = 0
When the object impacts the ground, its potential energy will be zero, having been entirely converted into kinetic energy:
U_final = 0
K_final = 1/2 mv²
Setting the initial mechanical energy equal to the final mechanical energy yields:
mgh = 1/2 mv²
Notably, we can simplify this equation by canceling out the mass (m), provided it is non-zero:
gh = 1/2 v²
4. Solving for Initial Velocity
The next step is to solve for the initial velocity (v) using the established relation. Manipulating the equation provides:
v² = 2gh
Taking the square root of both sides, we arrive at the equation for initial velocity:
v = √(2gh)
Thus, we have derived an elegant formula, allowing us to calculate the initial velocity of an object that falls freely from a specific height. Understanding the implications of this equation can provoke a transformative perspective on how physics governs real-world scenarios.
5. Real-World Applications
The utility of this foundational principle extends far beyond the academic milieu. Engineers and architects leverage these principles to design structures capable of withstanding dynamic forces, ensuring safety and stability. In sports science, understanding the initial velocities of projectiles aids in optimizing athletic performance—consider the basketball player calculating the right angle and speed for a successful shot.
Moreover, conservation of energy principles are invaluable in environmental sciences, where they assist in understanding energy flows within ecosystems and the implications of energy conversion in addressing climate change. When designing sustainable systems, knowing how energy shifts—like converting potential energy from water bodies into kinetic energy in hydroelectric plants—can impact energy consumption strategies and conservation efforts.
6. Experimental Verification
To deepen comprehension, practical experimentation can yield insightful verification of these theoretical concepts. One might conduct an experiment by dropping a ball from various heights while measuring the time taken to reach the ground. By applying the derived formula and comparing results, one can cultivate a deeper understanding of the interplay between theory and practice, rendering abstract concepts tangible.
7. Conclusion: Embracing the Shift
Ultimately, mastering the basics of finding initial velocity through the conservation of energy not only enriches one’s physics knowledge but also sparks curiosity about the broader implications in various fields. This understanding engenders a mindset capable of appreciating the intricate dance of forces at play in our environment, fostering an awareness of how physics underpins our physical world and urging the exploration of sustainable innovations. With these principles at the forefront, we can navigate toward a more informed perspective on energy utilization and conservation, ultimately aiding in the quest for a sustainable future.