Have you ever been on a roller coaster and wondered how fast you were going at that exhilarating moment when you plummet down a steep drop? The sensation of speeding through curves and loops is not just thrilling; it also presents a fascinating application of physics, particularly the concept of conservation of energy. In this ultimate guide, we will explore how to find speed in conservation of energy problems, emphasizing key concepts that will arm you with the necessary tools to crack such challenges. Let’s embark on this intellectual journey!
At the heart of conservation of energy lies the principle that energy cannot be created or destroyed but only transformed from one form to another. In classical mechanics, this typically translates to potential energy transforming into kinetic energy, and vice versa. The playful question arises: How can we quantify speed using this principle? This guide will walk you through the essential steps and considerations.
Understanding Energy Forms
Before diving into mathematical calculations, we must understand the two primary forms of energy involved in motion-related problems:
- Kinetic Energy (KE): This is the energy of motion, given by the equation KE = 1/2 mv², where m represents mass and v represents velocity. As an object’s speed increases, so does its kinetic energy, exponentially.
- Potential Energy (PE): This energy is stored due to an object’s position or configuration. For gravitational potential energy near Earth’s surface, the formula is PE = mgh, where g is the acceleration due to gravity (approximately 9.81 m/s²) and h is the height above a reference point.
In most conservation of energy problems, especially those involving roller coasters or free-falling objects, the interplay between these two forms of energy allows us to infer speed.
Setting Up the Conservation Equation
Once you grasp these energy concepts, setting up the conservation of energy equation becomes your next step. The law states that the total mechanical energy of a system remains constant in the absence of non-conservative forces, such as friction. Thus, the initial mechanical energy (potential and kinetic) will equal the final mechanical energy.
The general form of the conservation of energy equation can be expressed as follows:
PE_initial + KE_initial = PE_final + KE_final
This equation serves as the foundation upon which you’ll build your calculations. Let’s see how to apply it practically.
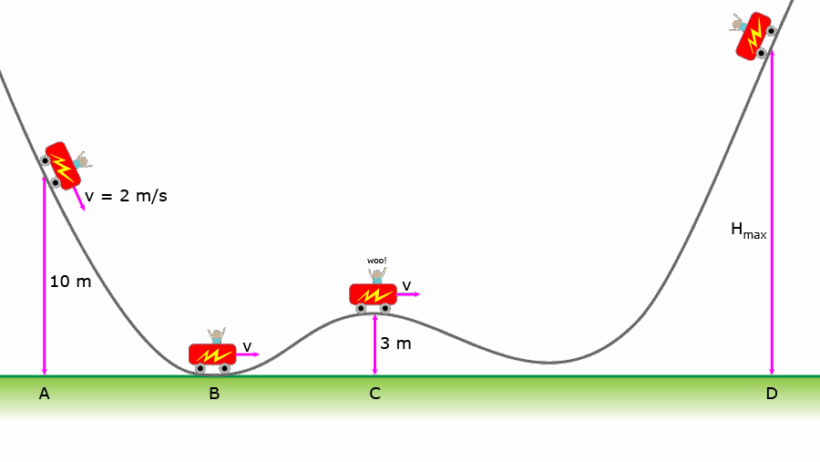
Example Scenario: Roller Coaster at Height
Consider a roller coaster that starts at a height of 50 meters and is initially at rest. Let’s determine the speed of the coaster as it descends to ground level (h = 0). Using the conservation of energy, we can calculate its speed at the lowest point:
- Calculate initial potential energy (PE_initial):
PE_initial = mgh = mg(50)
- Calculate initial kinetic energy (KE_initial):
Since it’s at rest, KE_initial = 0
- Calculate final potential energy (PE_final):
PE_final = mg(0) = 0
- Set the conservation equation:
mg(50) + 0 = 0 + 1/2 mv²
- Simplifying, you find:
50g = 1/2 v²
Rearranging gives:
v² = 100gTaking the square root leads to the final expression for speed:
v = √(100g).
The numerical value for g allows you to finalize the calculation. By substituting, you find the speed at the ground level, which showcases the conversion of potential energy into kinetic energy beautifully.
Handling Friction and Non-Conservative Forces
Real-world problems are rarely ideal; friction, air resistance, and other non-conservative forces can complicate the equation. These forces dissipate energy, thus altering the total mechanical energy of the system. If you’re presented with such conditions, modifications to the conservation equation must be made to account for the work done by these forces. The equation then takes the form:
PE_initial + KE_initial = PE_final + KE_final + Work_done_by_friction
Ignoring these forces in academic problems may simplify your calculations, but it’s vital to recognize their impact in practical applications. For instance, a roller coaster in a real amusement park might not reach the theoretical speed calculated above due to friction between the tracks and the cars.
Conclusion: Synthesizing Knowledge
The journey of understanding how to find speed through conservation of energy problems reveals a confluence of exciting concepts in physics. By mastering the transformation between potential and kinetic energy and how to manipulate the conservation equations, you’re not only preparing for exams but also equipping yourself with practical knowledge.
The next time you find yourself atop a roller coaster, reflecting on that impending drop, remember: the thrill isn’t just in the ride, but in the remarkable physics and energy transformations occurring all around you. Now, go forth and tackle conservation of energy problems with confidence and intellectual curiosity!