Understanding the conservation of energy through the lens of the Lagrangian method can seem daunting at first glance. But what if you could unlock the secrets of your mechanical system without unnecessary complexity? Let’s dive into the intricacies and determine how you can verify the conservation of energy using this powerful analytical tool.
The Lagrangian method is a cornerstone of classical mechanics that offers a systematic procedure for analyzing dynamics. It is derived from the action principle, which posits that the path taken by a system between two points in time is the one for which the action integral is extremized. This is characterized by the Lagrangian function, L, which is defined as the difference between kinetic energy, T, and potential energy, V:
L = T – V
Now, how can we ascertain whether energy is conserved in a mechanical system? A playful challenge enters here: Can you pinpoint moments in the motion where energy seems to simply vanish or reappear? The key lies in analyzing the equations derived from the Lagrangian function.
To determine if energy is conserved, one must first engage with the Euler-Lagrange equations, which arise from the principle of least action. These equations relate the derivatives of the Lagrangian to the generalized coordinates of the system. The Euler-Lagrange equation is expressed as follows:
d/dt(∂L/∂(dq/dt)) - ∂L/∂q = 0
Here, q represents the generalized coordinates of the system, and dq/dt are the generalized velocities. By solving these equations, one can derive the motion of the system—but the question of energy conservation persists.
For a system where the Lagrangian does not explicitly depend on time, the conservation of energy can be established. This is due to the property that if a variable does not appear in a system’s Lagrangian, then the corresponding momentum is conserved. Mathematically, the total energy E can be obtained from the Lagrangian as follows:
E = T + V
In many practical systems, particularly conservative systems, kinetic and potential energies transform into one another without a loss in total energy. This leads us to a fundamental understanding: if the energy derived from the Lagrangian remains constant over time, energy is conserved.
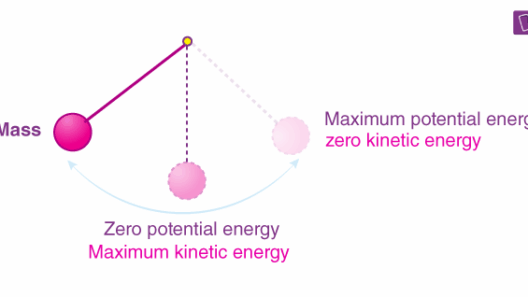
Let’s consider a tangible example, a simple pendulum—a classic physics demonstration. The Lagrangian can be expressed as:
L = T - V = (1/2) m l² (dθ/dt)² - m g l (1 - cos(θ))
In this formula, l is the pendulum length, g is the acceleration due to gravity, and θ is the angular displacement. By applying the Euler-Lagrange equation, we can derive the equations of motion. As the pendulum swings, potential energy is highest at the peak and kinetic energy is highest at the lowest point. By examining these transitions, the meticulous relationship between them showcases energy conservation in action.
However, what if external forces are introduced into the system? In such cases, the Lagrangian method can still illuminate the situation, but the interpretation alters. When dissipative forces are present, such as friction or air resistance, energy is not conserved in a closed sense. Instead, energy transformations occur where mechanical energy is lost to heat or deformation. A modified approach is needed to incorporate non-conservative forces—one can adapt the Lagrangian to include work done by external forces, requiring a deeper analysis.
Another interesting facet is when we deal with systems characterized by symmetry. Noether’s theorem, a profound result in theoretical physics, states that every differentiable symmetry of the action of a physical system corresponds to a conserved quantity. In contexts where the Lagrangian retains symmetry concerning time, energy conservation emerges automatically, offering a philosophical underpinning to the practical calculations.
Now, imagine you are tasked with a project that involves simulating a physical system. How would you ensure that energy remains conserved through your computational model? The verification requires diligence. You must regularly compute both the kinetic and potential energies throughout the simulation’s progression and maintain an awareness of external influences that could disrupt the balance.
The Lagrangian method thus serves as a dual compass— guiding you through both theoretical contemplations and practical applications. Tracking conservation of energy demands not merely the application of formulas but an understanding of the underlying physical interactions at play in your system. Every force, every transformation carries significance, shaping the trajectory of the total energy.
Ultimately, energy conservation is a fundamental principle that resonates across various disciplines in physics. Using the Lagrangian method provides a robust framework to validate this principle intricately. As you approach mechanical systems with a keen eye, you’ll find that the dance of kinetic and potential energies creates a symphony that is, ideally, harmonious and conserved.
So, when engaging with the elegance of dynamics through the lens of Lagrangian mechanics, remember: while the mathematics can appear abstract, the underlying physics remains grounded. Engaging consistently with the implications of energy conservation will sharpen both your analytical skills and your intuition about complex systems. The next time you witness a pendulum’s swing, ask yourself, is the energy conserved? The answer lies not just in calculations but in understanding the graceful interplay of forces acting upon it.