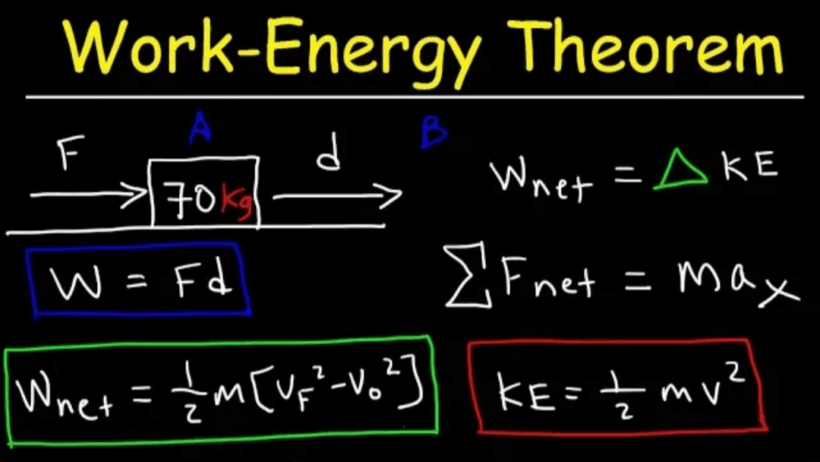
The Conservation of Energy Theorem is akin to a symphony in the grand orchestra of physics. It is orchestral harmony, where every note—representing potential energy, kinetic energy, thermal energy, and other forms—must be meticulously balanced. Understanding when to employ this theorem is vital for solving various physical problems, ranging from simple mechanics to intricate energy systems. This guide elucidates the principles surrounding the application of the Conservation of Energy Theorem, weaving together practical advice with illustrative examples.
Understanding Energy Forms
To appreciate the Conservation of Energy Theorem, one must first understand the diverse manifestations of energy. Broadly speaking, energy exists in two primary forms: potential and kinetic. Potential energy, often likened to a coiled spring, represents stored energy due to an object’s position—gravitational potential energy is a prominent example. Conversely, kinetic energy, akin to a flowing river, symbolizes energy derived from motion. It is imperative to discern these forms, as the theorem posits that the total energy in a closed system remains constant; it merely transforms from one form to another.
Recognizing Closed Systems
A fundamental prerequisite for applying the Conservation of Energy Theorem is identifying a closed system—an entity where no energy enters or exits. Picture a pristine ecosystem, where energy flows are self-contained and interactive, embodying the principle of conservation. Assessing the boundaries of the system is crucial; consider whether forces such as friction or air resistance might introduce external energy losses. If so, modifications to the raw approach may be required to account for these dissipative forces.
A Step-by-Step Approach
To astutely navigate scenarios necessitating the Conservation of Energy Theorem, one can follow a systematic methodology:
- Identify the Energy Forms: In the scenario at hand, catalog the forms of energy present—both initial and final states. For instance, in the case of a pendulum, assess its highest point for potential energy and its lowest for kinetic energy.
- Set the System Boundaries: Clearly delineate the boundaries of the system. If considering a roller coaster, visualize the tracks and cars as the defined space where energy transformations will be analyzed.
- Establish Energy Equations: Express the conservation principle mathematically. For the pendulum example, equate the gravitational potential energy at the highest point to the kinetic energy at the lowest point, giving you the formula: mgh = ½ mv².
- Solve for Unknowns: With equations in place, solve for any unknown variables. This may involve algebraic manipulation or utilizing additional relationships, such as those involving velocity or mass.
Recognizing the Limits
Utilizing the theorem is not without limitations. In real-world applications, energy is seldom conserved perfectly due to non-conservative forces such as frictional heat loss or air drag. It’s imperative to acknowledge these factors which can obfuscate calculations. When faced with such complexities, consider whether it is appropriate to integrate energy losses into your calculations or whether an alternate approach—such as applying Newton’s laws or examining work done—might yield more accurate insights.
Practical Applications
Real-world applications of the Conservation of Energy Theorem abound, illuminating its relevance across myriad contexts:
- Roller Coasters: The initial height of a roller coaster determines the velocity that can be achieved during descents. This hydraulic equation governs the exhilarating rush of speed.
- Hydroelectric Power Plants: In these installations, gravitational potential energy of water is converted into kinetic energy as it descends, driving turbines to generate electricity. Understanding this transformation is pivotal for optimizing energy efficiency.
- Mechanical Systems: Elevators embody the theorem as they convert electrical energy to mechanical energy. A detailed analysis of energy distribution allows engineers to enhance the overall system performance.
The Pursuit of Energy Efficiency
In an age where energy efficiency and conservation are paramount, employing the Conservation of Energy Theorem serves as an indispensable tool for engineers, architects, and environmentalists alike. Recognizing the implications of energy usage fosters a deeper appreciation for sustainability. Just as nature meticulously balances energy within ecosystems, so too must human systems uphold this principle by optimizing designs and practices that minimize waste.
A Metaphor for Mindfulness
Imagine the universe as a majestic tapestry, where each thread represents a unit of energy woven into existence. The Conservation of Energy Theorem is the loom upon which this tapestry is held. By understanding its tenets, one can learn to appreciate the intricate interconnections of energy—how it flows, transforms, and sustains life. Applying this theorem is not merely about calculations; it’s about embodying a mindful approach to problem-solving—an approach that emphasizes harmony over chaos, enlightening our pursuit of balance in energy consumption and conservation.
Conclusion
In conclusion, the Conservation of Energy Theorem serves as a guiding principle that underpins much of the physical world. By astutely recognizing when to apply this theorem, one can unravel complex problems within a myriad of contexts, all while nurturing a deeper connection with the principles that govern life itself. Embracing this understanding not only enhances technical prowess but reinforces a collective responsibility to cherish and wield energy wisely for our world’s future.