Conservation of energy is a fundamental principle of physics, underpinning almost all natural phenomena. Among the myriad of systems exemplifying this principle, the pendulum is a classic and accessible demonstration. Not only does the pendulum captivate with its rhythmic oscillation, but it also reveals deeper insights into energy transformations. This step-by-step tutorial aims to elucidate how to prove the conservation of energy in a pendulum system.
Understanding the Basics
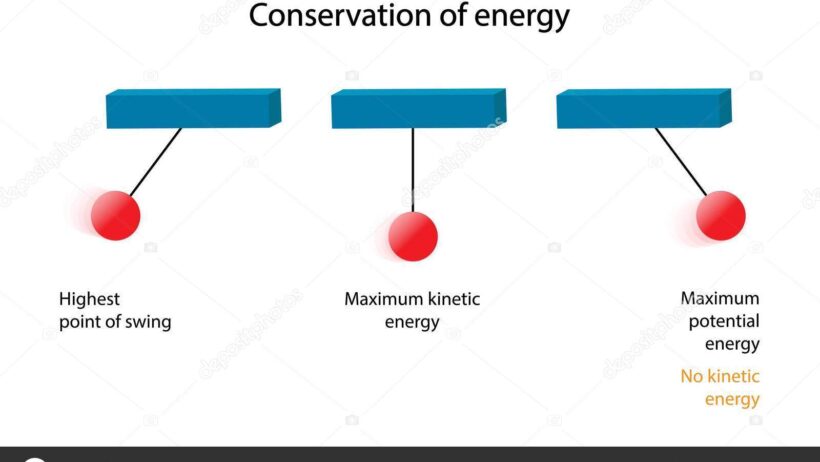
A pendulum consists of a weight, called a bob, attached to a string or rod, which pivots at a fixed point. As the pendulum swings, it alternately converts potential energy into kinetic energy and back again. The total mechanical energy—comprising these two forms—remains constant in the absence of external forces such as friction or air resistance. This notion of energy conservation is both profound and essential for comprehending various physical systems.
Before delving into the experimental procedure, we must outline the relevant concepts:
- Potential Energy (PE): This is the energy stored in an object due to its position. For a pendulum, the highest point of swing represents maximum potential energy. It can be calculated using the formula PE = mgh, where m is the mass of the bob, g is the acceleration due to gravity, and h is the height above a reference point.
- Kinetic Energy (KE): This is the energy of motion. The pendulum reaches its maximum kinetic energy at the lowest point of the swing, expressed as KE = 0.5mv², where v is the speed of the bob.
- Mechanical Energy (ME): The total energy of the pendulum system, given by ME = PE + KE.
Materials Needed
To conduct this experiment, gather the following materials:
- A sturdy pendulum setup, which can be created using a weighted object (like a small bag of sand or a heavy ball) and a string.
- A protractor for measuring angles of displacement.
- A stopwatch or timer to measure the time of swings.
- A ruler to measure the height of the pendulum bob during its swing.
- A calculator to assist with calculations of energy values.
Experimental Procedure
- Set Up the Pendulum: Securely suspend the pendulum from a fixed pivot point, ensuring that it is free to swing without obstruction. The length of the string should be measured accurately from the pivot to the center of the bob.
- Measure Initial Height: Pull the bob to one side and determine the initial height h from which it will be released. Use the ruler to measure this height relative to the lowest point of the swing.
- Release and Observe: Without pushing, release the bob and allow it to swing freely. Observe the motion and record the time taken for a set number of complete swings.
- Calculate Potential Energy: At the starting position (highest point), calculate the potential energy using the formula PE = mgh. Plug in your measured values of mass, gravity (9.81 m/s²), and height.
- Determine the Kinetic Energy: At the lowest point of the swing, calculate the kinetic energy using the formula KE = 0.5mv². To find v, one may use the periodic time derived from the recorded swing time.
- Verify Conservation: To validate conservation of energy, compare the calculated values of PE and KE. The total mechanical energy at the highest point should approximately equal the total mechanical energy at the lowest point.
Data Analysis
Upon performing the experiment, methodically analyze the results. In an ideal scenario devoid of friction, the sum of potential and kinetic energies at any given point of the pendulum’s swing should remain constant. Minor discrepancies may arise due to air resistance and friction at the pivot, yet they offer an opportunity to explore real-world applications of energy conservation. Such observations can lead to discussions about energy losses in everyday systems.
Discussion and Conclusion
Through this experiment, one can visually and mathematically grasp the conservation of energy principle in a pendulum. The transformation of energy types—from potential to kinetic and back again—illustrates a core tenet of physics that resonates beyond the pendulum itself. Understanding these principles emphasizes humanity’s responsibility to consider energy conservation in its myriad forms, including its implications for environmental sustainability and climate action.
The pendulum’s simple oscillatory motion belies its complex underpinnings in physics. It is precisely this interplay of energy conversion that captivates and educates, encouraging future generations to ponder the intricate dance of forces that govern our world. The pendulum is a mere fragment of a larger tapestry, a reminder that the principles of conservation extend into our broader interactions with the earth and the energy systems that sustain life.