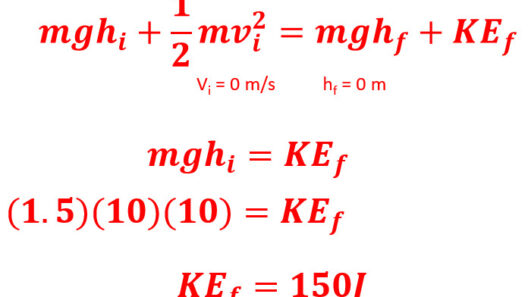The realm of physics is full of intriguing principles that govern the universe. One such principle is the Law of Conservation of Mechanical Energy. Have you ever wondered how a roller coaster can soar upwards only to plummet downwards? What if we could challenge this notion? Can we demonstrate that the total mechanical energy—kinetic plus potential—remains constant throughout its motion? This notion not only sparks curiosity but also invites empirical exploration into fundamental physics.
To understand how to prove the Law of Conservation of Mechanical Energy, we must first define mechanical energy itself. Mechanical energy is the sum of potential energy (PE) and kinetic energy (KE) in a given system. Potential energy is stored energy, dependent on the position of an object relative to a reference point, while kinetic energy is the energy of an object in motion, directly influenced by its mass and the square of its velocity.
Mathematically, the conservation of mechanical energy can be summarized by the equation: ME = PE + KE, where ME is the total mechanical energy. The law posits that in the absence of non-conservative forces (like friction or air resistance), the total mechanical energy of a system remains constant.
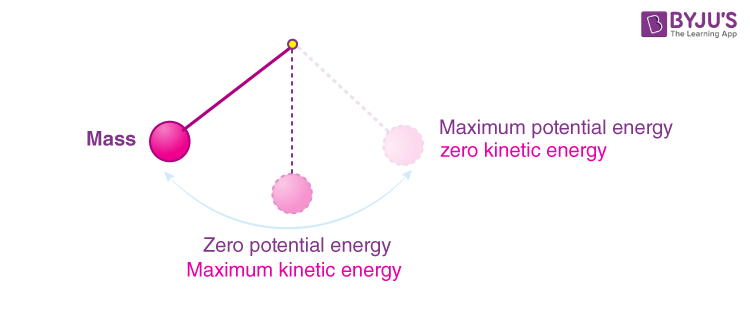
Let’s set the stage for an experiment. Imagine a simple setup involving a pendulum. The pendulum, consisting of a bob attached to a string, is an excellent demonstrative apparatus. In order to provide a clear understanding, we would need to measure both potential and kinetic energy at various points during the pendulum’s swing.
At the highest point of the swing, the pendulum possesses maximum potential energy and a minimum kinetic energy—essentially zero as it momentarily halts before descending. This is because all the energy has been converted to potential energy: PE = mgh, where m is mass, g is gravitational acceleration, and h is height above the reference point.
As the pendulum swings downwards, potential energy is converted into kinetic energy. At the lowest point of the swing, the height is zero, resulting in no potential energy, yet the kinetic energy here is at its peak, given by the equation KE = ½mv². This kinetic energy represents the energy of motion as the pendulum travels the fastest.
To conduct the experiment, we need to precisely measure the height of the pendulum at its peak and calculate the potential energy. Then, we must measure the speed at the lower point to calculate kinetic energy. Collecting these data points enables one to analyze how energy is conserved throughout the pendulum’s motion.
The results should reflect that the total mechanical energy at the highest point equals the total mechanical energy at the lowest point, thereby supporting the conservation law. However, should we observe discrepancies, it may indicate the influence of air resistance or friction acting as non-conservative forces, emphasizing the principle’s dependence on ideal conditions.
Course-correcting for non-ideal scenarios gives rise to an important discussion: how do we isolate conservative forces? This leads us into various methods for minimizing resistance effects—such as performing the experiment in a vacuum or utilizing low-friction materials. While these conditions might seem extreme, they establish the foundational scenarios where the conservation of mechanical energy most accurately holds.
Engaging with the Concept: Why Does It Matter?
Understanding how to prove the Law of Conservation of Mechanical Energy is not merely an academic endeavor. This principle is fundamental in various applications across engineering, environmental science, and even in our everyday lives. By comprehending these principles, one can better grasp energy efficiency, mechanics related to vehicles, roller coasters, and even natural ecosystems.
For instance, when considering renewable energy systems such as wind turbines or hydroelectric plants, the conservation of mechanical energy plays a crucial role in calculating and optimizing energy output. These systems convert mechanical energy derived from natural forces into electrical energy, showcasing a practical application of the principle we have been discussing.
Moreover, the application extends to climate change challenges. By understanding energy conservation, scientists and engineers can more efficiently harness natural energy sources, mitigate waste, and create sustainable solutions to reduce fossil fuel reliance, ultimately aiding in the fight against climate change.
In conclusion, the Law of Conservation of Mechanical Energy serves as a cornerstone in our understanding of physics and its real-world applications. Through experiments, we can not only validate this law but appreciate its implications in various fields. To adequately demonstrate this principle, one must embrace meticulous measurement, critically assess environmental factors, and apply a framework of ideal conditions.
Ultimately, engaging with physics enriches our understanding of how energy transforms and interacts in our world, guiding us towards sustainable practices that honor the delicate balance of our environment. So, the next time you see a roller coaster in motion, remember the invisible dance of energy—both daunting and delightful—which undeniably adheres to the law of conservation, painting a vibrant picture of physics in action.