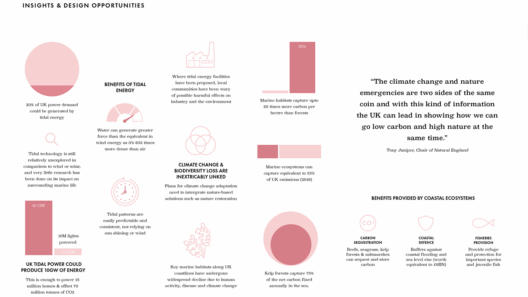
The concept of energy conservation is not merely an abstract principle; it is an omnipresent phenomenon that governs the physical world around us. Understanding how to set up a conservation of energy equation is crucial for the intersection of physics and real-world applications. This challenge engages students, professionals, and enthusiasts, invoking a fascination with the underlying energy transformations that occur in various systems. This article will guide you through the essential components of crafting a conservation of energy equation, while elucidating the significance of each element involved.
To embark on this scientific journey, one must first grasp the fundamental principle of energy conservation. This law stipulates that energy cannot be created or destroyed; it merely transforms from one form to another. The mathematical expression of this principle can take many forms, but it consistently centers on the concept of total mechanical energy: the sum of kinetic and potential energies in a system.
Understanding Kinetic and Potential Energy
Kinetic energy (KE) is defined as the energy of an object in motion, mathematically represented by the formula KE = ½mv², where m signifies mass and v denotes velocity. This expression highlights the quadratic relationship between velocity and kinetic energy, suggesting that small changes in speed can lead to significant variations in energy.
On the opposite spectrum lies potential energy (PE), a form of stored energy dependent on an object’s position or configuration. The most common type of potential energy is gravitational potential energy, denoted as PE = mgh, where g represents the acceleration due to gravity, and h indicates the height above a reference point. Understanding these energy forms sets the foundation for applying the conservation of energy principle.
Setting Up the Conservation of Energy Equation
To devise a conservation of energy equation, one must consider a closed system where external forces do not perform work. The total mechanical energy at one point in time must equate to the total mechanical energy at another point. Hence, we derive the equation:
KE_initial + PE_initial = KE_final + PE_final
This equation encapsulates the fundamental idea that the initial kinetic and potential energy of a system should equal the final kinetic and potential energy, illustrating that energy is conserved through the interaction of these forms. However, this formula also serves as a gateway to more complex scenarios involving non-conservative forces, such as friction.
Incorporating Non-conservative Forces
In many real-world applications, energy is transformed into heat due to friction or air resistance, resulting in energy dissipation. To account for these losses, it becomes essential to introduce the work done by non-conservative forces into the equation. This adjustment leads to:
KE_initial + PE_initial + W_nc = KE_final + PE_final
Here, W_nc denotes the work performed by non-conservative forces. This addition accentuates another layer of complexity, compelling one to analyze how forces affect energy distributions within the system.
Practical Applications and Examples
Understanding the conservation of energy equation extends beyond academic pursuits; it has practical implications in various fields. For instance, consider a roller coaster. At its highest point, the ride has maximum potential energy and minimal kinetic energy. As it descends, potential energy is converted to kinetic energy, offering a thrilling experience while adhering to the conservation of energy principle.
Another compelling scenario involves a pendulum swinging. At the apex of its swing, the pendulum possesses significant potential energy. As it descends, that potential energy gradually converts to kinetic energy, maximizing just as it reaches the lowest point. This cyclical pattern exemplifies energy transformations, illustrating fundamental physical principles in an engaging manner.
Critical Thinking and Deeper Understanding
Engaging deeply with the conservation of energy equation can invoke a sense of wonder about the underlying mechanics of our universe. Why does a thrown ball come to rest? What governs the rhythm of a pendulum? Exploring these questions fosters a more profound curiosity about the nature of forces and energy in our environment. The beauty of physics is encapsulated not just in equations, but in the harmonious dance of energy transformations that dictate motion, stability, and interaction.
Conclusion: Embracing Energy Conservation
In summary, setting up a conservation of energy equation requires a solid understanding of kinetic and potential energy, as well as the ability to incorporate external influences like non-conservative forces. The applications of these equations span diverse practical situations, from simple mechanical systems to complex engineering designs. Understanding these principles is not just an academic exercise; it is an invitation to observe and appreciate the elegance and order of the universe. Through this lens, one can explore how energy flows and transforms, anchoring our understanding of the physical world to fundamental principles that govern reality itself.