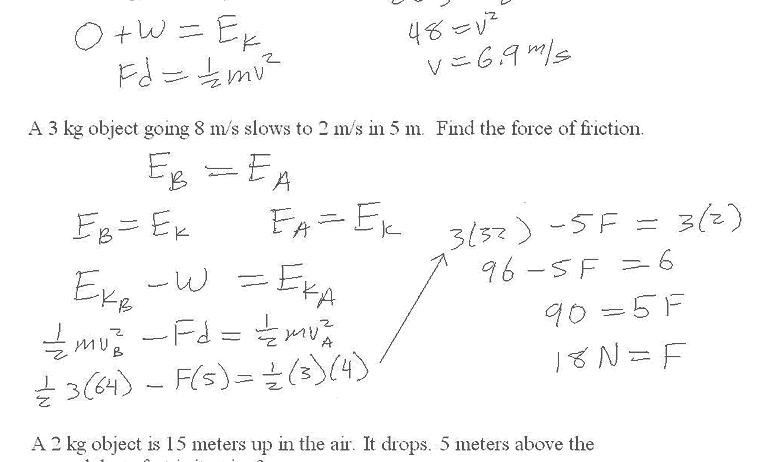Conservation of mechanical energy is a fundamental principle in physics, illuminating the fascinating interplay between potential energy and kinetic energy. This principle asserts that in an isolated system, the total mechanical energy remains constant if only conservative forces are acting. Understanding this concept can evoke curiosity about the myriad of phenomena surrounding motion and energy transfer in our environment. This guide aims to simplify the approach to solving problems related to conservation of mechanical energy, paving the way for a more profound comprehension of the world around us.
Understanding the Basics
To embark on this journey, it’s crucial to grasp the foundational elements. Mechanical energy is the sum of kinetic energy (KE), the energy of motion, and potential energy (PE), the energy stored due to an object’s position or configuration. Mathematically, this can be expressed as:
ME = KE + PE = (1/2)mv² + mgh
Where:
- m = mass of the object (in kg)
- v = velocity of the object (in m/s)
- g = acceleration due to gravity (approximately 9.81 m/s² on Earth)
- h = height above a reference point (in meters)
The Law in Action
The beauty of the conservation principle lies in its application across various scenarios—from roller coasters swooping down and up hills to pendulums gracefully oscillating. Consider a simple example: a ball thrown vertically upward. At its peak, the kinetic energy is at a minimum (momentarily zero), while potential energy is maximized. Upon its descent, potential energy converts back to kinetic energy, demonstrating the seamless transformation between the two forms of energy.
Solving Problems: Step by Step Approach
A systematic approach will enable the resolution of problems involving conservation of mechanical energy.
Step 1: Analyze the System
The first step involves identifying the system and external forces. Decide whether any non-conservative forces (like friction) are present. If so, they could alter the total mechanical energy, and thus, the conservation principle may not hold.
Step 2: Identify Energy States
Spot the key points in your problem where you can evaluate the energies. For example, consider the highest point of a motion (maximum potential energy) and the point just before impact (maximum kinetic energy). Sketching a diagram can help visualize these energy states.
Step 3: Apply the Conservation Equation
Once the energies are established, apply the conservation of mechanical energy equation:
KE_initial + PE_initial = KE_final + PE_final
This equation is your compass, guiding you through calculations. Substitute the known values and solve for the unknown variable based on what the problem asks.
Step 4: Solve for Unknowns
Carefully manipulate the equation to isolate the unknown variable. This might involve algebraic rearrangements, especially if you’re solving for height or velocity. Be meticulous here; one minor error can lead to skewed results.
Step 5: Interpretation of Results
After calculating, interpret your results within the context of the physical scenario. Does it make sense? Encouraging critical thinking in relation to your findings is crucial. This reflection not only solidifies understanding but also transports knowledge into real-world applications.
Common Problems and Solutions
There are several classic problems that exemplify the conservation of mechanical energy. Here are a few:
- Free Fall: A rock dropped from a height transforms potential energy into kinetic energy as it plummets towards the ground. Calculate its velocity just before impact by equating PE at the top to KE at the bottom.
- Harmonic Oscillator: In a mass-spring system, observe how the energy oscillates between kinetic (when the mass is in motion) and potential (when the spring is either compressed or stretched).
- Roller Coaster: The design and thrill of a roller coaster depend on the conservation principle, balancing PE at high points and KE at low points. Calculate speed at the lowest point or height at the highest using the same approach.
Conclusion: A Revitalized Perspective
As we navigate through conservation of mechanical energy, it opens up a multitude of inquiries. How does energy conservation affect modern engineering, transport systems, or even environmental sustainability? With each problem solved, a deeper understanding emerges, fueling curiosity to explore more. In our rapidly changing world, recognizing the principles of energy conservation can inform more intelligent interactions with our surroundings. Consider how mechanical energy conservation encourages equilibrium—the balance we seek not only in physics but also in our environmental practices.
The next time you witness an object in motion, remember the invisible forces at play. They are the subtle reminders of the energy that binds our reality, awaiting your exploration and insight.