Understanding whether mechanical energy is conserved in a given situation requires a meticulous step-by-step analysis. It is akin to a detective unraveling a mystery, piecing together clues from the grand tapestry of physics to discern the underlying principles at work. At the heart of this exploration lies the fundamental concept that mechanical energy consists of two key components: kinetic energy (KE) and potential energy (PE).
Mechanical energy conservation can be illustrated through various scenarios, the most prominent being those involving systems devoid of external forces. To ascertain if mechanical energy is conserved, one must follow a structured approach, akin to a roadmap for navigating through the labyrinth of forces and interactions.
Step 1: Define the System
The first step in analyzing mechanical energy conservation is to define the system in question. Identifying the boundaries of the system allows for the isolation of variables. It’s pivotal to determine the objects involved and the environment surrounding them. This step is analogous to establishing the parameters of a crime scene before investigating further.
For instance, consider a swinging pendulum. The system encompasses the pendulum bob and the pivot point. Any forces acting on the bob, such as friction, can be viewed as interactions with the environment that may influence energy conservation.
Step 2: Identify Forces at Play
In many cases, the presence of non-conservative forces like friction indicates that mechanical energy will not be conserved. Here, the enigmatic nature of energy reveals itself: some energy is lost to the surroundings in non-recoverable forms, like heat.
Step 3: Calculate Initial Mechanical Energy
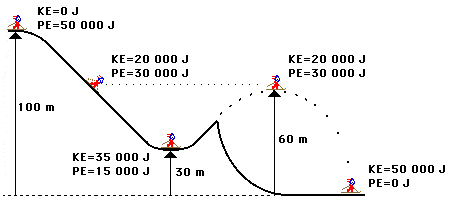
Once the system and its forces are identified, the next move is to calculate the initial mechanical energy. This involves summing the kinetic and potential energy at the beginning of the observation. Kinetic energy is calculated using the formula KE = 0.5 * m * v², where m is mass and v is velocity. Potential energy depends on the system’s context; in gravitational fields, it is calculated using PE = m * g * h, where g is the acceleration due to gravity, and h is height.
For instance, if a roller coaster is perched at the peak of a hill, it possesses potential energy relative to the ground, while its kinetic energy is negligible at that moment (assuming it’s momentarily at rest). So, the total mechanical energy can be computed before any descent occurs.
Step 4: Analyze Energy Changes
The subsequent step is to observe the changes in mechanical energy as the system evolves. As the pendulum swings or the roller coaster races down the hill, energy transforms between kinetic and potential forms. The conservation principle asserts that, in an ideal system devoid of external influences, the total mechanical energy remains constant.
However, if there are external influences—if the pendulum starts to slow down due to air resistance or if the roller coaster experiences friction against the tracks—then the total energy will decrease over time, indicating that mechanical energy is not conserved.
Step 5: Calculate Final Mechanical Energy
Once energy changes are analyzed, it is time to calculate the final mechanical energy of the system at a specific moment. This will involve re-assessing the kinetic and potential energies as the system reaches a new state. Ideally, in a frictionless environment, this step should yield a mechanical energy total equivalent to the initial calculation.
Continuing with the roller coaster metaphor, as it races downwards, potential energy converts to kinetic energy, resulting in increased speed. On reaching the bottom, potential energy decreases to its minimum, while kinetic energy peaks. Mathematically assuring that the sum remains the same in an ideal scenario showcases the beauty of energy conservation.
Step 6: Compare Initial and Final Mechanical Energy
The final step in this analysis involves a direct comparison between the initial and final mechanical energies of the system. If both values remain congruent, energy is conserved. If they differ significantly, it indicates energy losses attributed to external forces.
It is crucial to understand that energy, like a chameleon, adapts to its environment. Whether it transforms from one form to another or dissipates into the ether, the essence of energy is perpetually dynamic. By conducting the above steps, one can ascertain the fate of mechanical energy within a system as it dances through kinetic and potential realms.
Conclusion: The Intrigue of Conservation
Grasping the nuances of mechanical energy conservation requires not only analytical acumen but an appreciation for the intricate relations between energy forms. By expertly navigating through the established steps, one gains insight into the universal spectacle of energy in its myriad forms. The thrill of unveiling energy’s secrets beckons scientists and laypeople alike into a captivating world of discovery. Ultimately, understanding how to discern the conservation of mechanical energy enriches our appreciation of the natural phenomena that govern our existence.