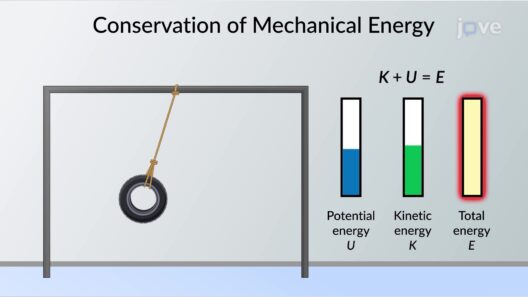
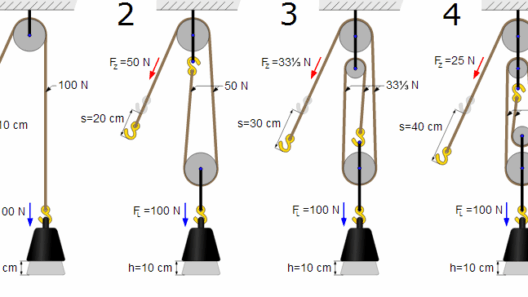
In the grand tapestry of physics, momentum and kinetic energy represent two intricate threads woven with precision. Understanding their conservation offers crucial insights into the dynamics of systems—whether they are as simple as a game of pool or as complex as a celestial collision. The confluence of momentum and kinetic energy conservation not only reveals the efficiency of energy transfer but also acts as a barometer of physical interactions throughout the universe.
Momentum, defined as the product of mass and velocity, can be construed as the “quantity of motion.” Much like a river flowing steadily, momentum persists unless acted upon by an external force. By contrast, kinetic energy—the energy an object possesses due to its motion—could be likened to the potential of the river to generate power as it cascades down a waterfall. When contemplating the conservation of these two physical quantities, it is essential to navigate through the intricacies that dictate when and how they remain constant.
To decipher the interplay of momentum and kinetic energy, one must first distinguish between elastic and inelastic collisions. In an elastic collision, both momentum and kinetic energy are conserved. This scenario can be visualized as two perfectly bouncing rubber balls colliding and separating, retaining their speed and direction. Alternatively, in an inelastic collision, momentum remains conserved while kinetic energy dissipates as sound, heat, or deformation, much like a clay ball squished upon impact. Only in the realm of elastic collisions can we marvel at the art of physics in its purest form—where the dance of particles retains both their velocity and energy after the encounter.
One might ponder, how can we ascertain whether a collision is elastic or inelastic? A systematic approach can unveil the answer. First, start by measuring the individual masses and velocities of the colliding bodies both pre- and post-collision. The momentum before the collision can be calculated through the mathematical formula:
Momentum (p) = mass (m) x velocity (v)
By summing up the momentum vectors of all participating objects prior to the collision, we can subsequently evaluate the total momentum after the impact. If both the pre-collision and post-collision momentum values are equal, momentum conservation is validated.
Next comes the check for kinetic energy. The total kinetic energy before and after the collision can be evaluated using the formula:
Kinetic Energy (KE) = 0.5 x mass (m) x (velocity (v))²
Similar to momentum, if the kinetic energy totals before and after the collision match, we find ourselves in the realm of elastic collisions. Here lies a critical note: kinetic energy, unlike momentum, can transform into various forms of energy during collisions where deformation occurs, reflecting that not all interactions are equal in energy conservation.
A fascinating complexity arises when analyzing real-world situations, such as car accidents. In these encounters, kinetic energy is often converted into heat and sound, signaling the collision’s inelastic nature. Momentum, however, remains a steadfast companion, guiding investigators in reconstructing accident scenes, providing insight into speeds and directions prior to impact.
Another striking example can be observed in celestial phenomena. The collisions of asteroids, for instance, might offer scenarios where both momentum and kinetic energy are fleetingly conserved, yet their manifestation transforms radically. The awe-inspiring fusion of an asteroid with a planet showcases how energy can be redistributed and matter significantly altered yet momentum flows through these cosmic interactions uninterrupted. Understanding these phenomena deepens the appreciation for the universe’s balance.
In everyday life, the conservation laws reveal their importance as we engage in sports. A perfectly executed shot in billiards can exhibit both momentum and kinetic energy conservation, as the cue ball strikes the other balls, sending them off in calculated trajectories. This knowledge empowers players to harness physics in strategy—akin to wielding tools from a toolbox of laws governing our existence.
As we delve into the implications of conservation laws, it is also imperative to consider the philosophical ramifications. At times, the pursuit of understanding kinetic energy and momentum conservation parallels the quest for balance and harmony. In ecosystems, energy conservation equates to sustainability—a delicate ballet of flora and fauna symbiotically interwoven. The movement of species, much like that of particles, reflects a commitment to maintaining equilibrium, conserving momentum while allowing energy to dissipate judiciously.
Ultimately, the conclusion of this exploration unveils a captivating yet complex narrative woven around momentum and kinetic energy conservation. Recognizing when they are simultaneously conserved hinges on comprehensive measurement and evaluation during interactions. While both quantities bear unique identities, their relationship embodies the fundamental principles of motion. By harnessing this profound understanding, we can unlock deeper insights into the workings of our universe, relish the fragility of our ecological balance, and celebrate the symphony of conservation that governs all matter.