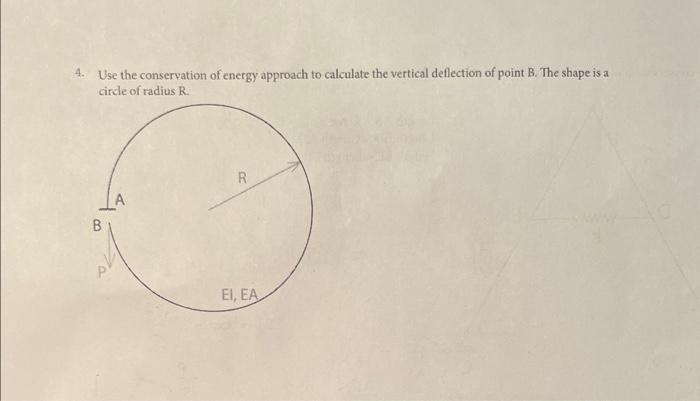
Conservation of energy is a fundamental principle in physics that applies to many situations, including mechanical systems. It states that energy cannot be created or destroyed, only transformed from one form to another. In the context of vertical deflection, where an object is subjected to forces like gravity, understanding energy transformations is crucial for accurate calculations.
Have you ever wondered about the height at which a projectile thrown into the air will reach its peak before falling back down? This playful inquiry leads to a wider challenge: accurately predicting the vertical deflection of the object based on its initial energy. To address this, we must delve into the mechanics of energy conservation.
When an object is thrown upward, it begins with kinetic energy, which is the energy of motion. This kinetic energy is given by the equation:
K.E. = ½ mv²
In this equation, ‘m’ represents mass, and ‘v’ is the velocity of the object. As the object rises, it loses speed due to the gravitational pull acting on it. Consequently, some of its kinetic energy is converted into gravitational potential energy (G.P.E.), which is given by:
G.P.E. = mgh
Here, ‘g’ is the acceleration due to gravity (approximately 9.81 m/s² on Earth), and ‘h’ is the height gained. The key concept is that at the peak of its trajectory, all of the initial kinetic energy has been transformed into potential energy. This leads to an essential relationship:
Initial K.E. = Final G.P.E.
Therefore, we can set the equations equal to each other, leading us to:
½ mv² = mgh
Notice how the mass ‘m’ can be simplified from both sides, which leads to:
½ v² = gh
This makes it possible to solve for height ‘h’:
h = ½ v²/g
Now, applying this equation helps us find the vertical deflection of any object subjected to an initial velocity. The height reached by the object is indicative of the vertical deflection it undergoes. Hence, the relationship between initial velocity and deflection is paramount for predicting the motion effectively.
Considering energy conservation not only enables computations for projectiles but also is applied in structures such as beams, where vertical deflection occurs due to applied loads. In civil and mechanical engineering, the concept of vertical deflection in beams under loading conditions becomes a matter of energy management. The mechanical energy associated with bending and stretching can be evaluated using the principles of potential energy stored in the material.
When a beam bends, it does so by distributing the applied load throughout the length and inducing internal stresses. The deformation that occurs can be analyzed through the relationship between the applied load, the beam’s material properties, and its geometry. The total strain energy in a beam can be established through integration based on its bending moment.
To calculate the vertical deflection of a simply supported beam subjected to a central point load, you can utilize the energy method. For such a scenario, the formula for deflection ‘δ’ can be given by:
δ = (PL³) / (48EI)
In the equation, ‘P’ represents the load applied at the center, ‘L’ is the length of the beam, ‘E’ is the modulus of elasticity of the material, and ‘I’ is the moment of inertia. This deflection formula arises from integrating the mechanical energy related to bending. As with projectiles, the energy associated with the load causes the beam to deflect vertically.
However, there’s always more than meets the eye. In practical applications, other factors such as material yield strength and boundary conditions significantly influence the actual deflection. Consequently, over-simplifying conditions can lead to inaccuracies. As professionals engage with these calculations, understanding all aspects ensures compliance with safety and operational standards, which is paramount.
Moreover, environmental conditions such as temperature and humidity can alter material properties, thereby influencing deflection outcomes. This reinforces the idea that while energy conservation gives us a powerful tool for calculation, the real-world implementation requires comprehensive analysis and regular assessments of material integrity.
In summary, the principle of conservation of energy provides a robust framework for calculating vertical deflection, whether for projectiles or structural elements. This principle, coupled with a detailed understanding of material behavior and environmental influences, equips engineers and scientists to make informed predictions about motion and structure alike. As we leverage these principles in our work, we not only aspire to fulfill our technical obligations but also to contribute to the broader goal of sustainability in practices that conserve our natural resources.