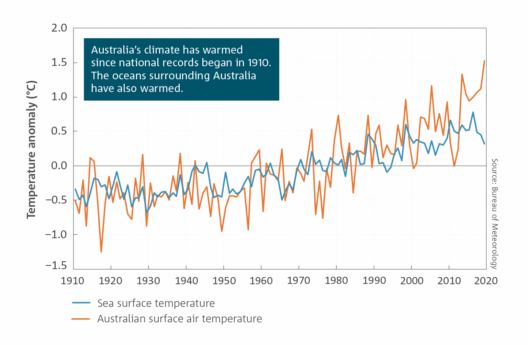
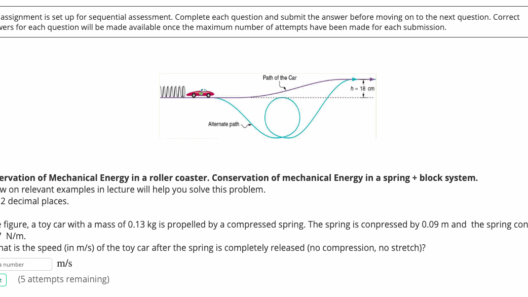
In the realm of classical mechanics, the principle of conservation of energy plays a pivotal role in the understanding of motion and force. Angular kinetic energy, a specific form of kinetic energy associated with rotational motion, raises intriguing questions regarding its conservation under various conditions. To comprehend whether angular kinetic energy is conserved, one must delve into fundamental concepts such as torque, angular momentum, and external influences.
First, it is essential to distinguish between linear kinetic energy and angular kinetic energy. Linear kinetic energy is defined as the energy possessed by an object due to its linear motion, quantified by the equation KE = ½mv², where m denotes mass and v represents linear velocity. Conversely, angular kinetic energy pertains to objects that rotate about an axis, and it can be expressed by the formula KEangular = ½Iω², with I representing the moment of inertia and ω the angular velocity. This distinction lays the groundwork for exploring energy conservation in rotational systems.
The conservation of angular kinetic energy hinges significantly on the absence of external torques. When a rigid body rotates without the influence of external forces, its angular momentum remains constant, according to the principle of conservation of angular momentum, which states that L = Iω, where L is angular momentum. In such closed systems, one can ascertain that angular kinetic energy is conserved.
However, the introduction of external torques complicates this scenario. For instance, if an object experiences a net torque, it results in a change in angular momentum, and thus angular kinetic energy may not be conserved. A classic example is a spinning top. As it rotates, friction between the top and the surface exerts a torque. This external torque causes the top to gradually lose energy to its surroundings, leading to a decrease in rotational speed and, subsequently, a loss of angular kinetic energy.
Another factor to consider is the conversion of energy types. In systems where energy transformations occur, such as in pendulums or rotating disks, the conservation of angular kinetic energy can coexist with variations in other forms of energy. In a pendulum swing, for example, the highest point represents maximum potential energy, while the lowest point denotes maximum kinetic energy. Although angular kinetic energy appears to fluctuate, the mechanical energy of the system is conserved in an ideal scenario without air resistance or friction.
To investigate real-world systems where angular kinetic energy is conserved, examples such as planetary motion and satellites come into play. The Earth, rotating around its axis and revolving around the sun, exemplifies a system where gravitational forces act as centripetal constraints, allowing angular momentum to be conserved. The angular kinetic energy associated with celestial bodies remains relatively stable due to the vastness of space, which minimizes external influences.
In examining isolated systems, one must also acknowledge forces such as internal friction within a rotating rigid body. For instance, the distribution of mass affects the moment of inertia, whereby alterations can lead to changes in angular velocity. While the total energy may remain constant, the transformation among various components (like vibrations or thermal energy) indicates that angular kinetic energy isn’t always preserved in its initial form.
A critical aspect of understanding angular kinetic energy conservation involves energy dissipation mechanisms. In engineering applications, for example, components like bearings and gears experience friction, which can lead to energy loss. The designs often incorporate strategies to minimize this dissipation, thereby optimizing performance by maintaining as much angular kinetic energy as possible throughout the rotational process.
Furthermore, the application of angular kinetic energy conservation principles extends into various fields such as sports science and biomechanics. Athletes often exploit these principles in activities like gymnastics or diving, where the body’s rotation can be strategically controlled to optimize performance outcomes. Coaches and trainers analyze angular momentum to enhance techniques that minimize energy loss, allowing athletes to execute movements with greater efficiency.
In consideration of all these factors, it becomes evident that the conservation of angular kinetic energy is nuanced. While in ideal circumstances, such as closed systems devoid of external torques, angular kinetic energy can be conserved effectively, real-world dynamics frequently necessitate a more complicated analysis. Factors like friction, mass distribution, and energy transformation underscore the complexities inherent in conservation laws.
In summary, the inquiry into whether angular kinetic energy is conserved unveils a rich tapestry of physical principles. The interplay between motion, energy types, and forces offers a comprehensive understanding of how angular kinetic energy behaves across various contexts. Through rigorous examination of these dynamics, one can appreciate not only the preservation of energy but also the artistry of motion in a world governed by fundamental forces.
Ultimately, while conservation may be thought of in absolute terms, the application of these principles calls for precise considerations of conditions and environments that influence the flow and transformation of energy. Analyzing angular kinetic energy in both theoretical and applied contexts illuminates larger questions about motion and energy within the universe.