Understanding the conservation of energy is fundamental to physics, particularly in the analysis of mechanical systems. The simple pendulum stands as a quintessential example in which energy conservation principles can be clearly observed and described. This exploration delves into how the simple pendulum operates under the law of conservation of energy, providing insights into its implications and real-world applications.
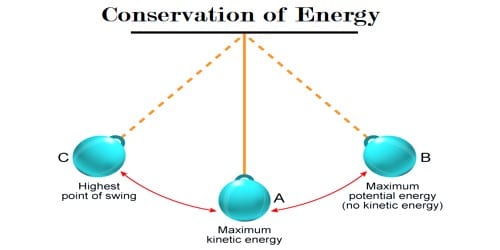
A simple pendulum consists of a mass, known as the bob, suspended from a fixed point by a string or rod of negligible mass. When released from an initial height, the pendulum swings back and forth, demonstrating periodic motion. The primary forces involved are gravity and tension, which contribute to the pendulum’s energy dynamics. Throughout its motion, the pendulum has two primary forms of mechanical energy: potential energy (PE) and kinetic energy (KE).
Potential energy is defined as the energy stored in an object due to its position. In the case of the simple pendulum, the highest point in its swing—the amplitude—represents the peak of potential energy. The formula for gravitational potential energy is given by:
PE = mgh
where m is mass, g is the acceleration due to gravity, and h is the height relative to the lowest point of the swing. At this maximum height, the pendulum is momentarily at rest, possessing only potential energy.
As the pendulum begins its descent, potential energy gradually transforms into kinetic energy, the energy of motion. Kinetic energy is expressed through the formula:
KE = 0.5mv²
where v is the velocity of the bob. As the pendulum swings downward, it accelerates due to gravitational force, culminating in maximum kinetic energy at the lowest point of the swing. At this juncture, the pendulum’s speed is at its zenith, while potential energy is at a minimum, theoretically zero if we choose the lowest point as the reference level.
This continuous conversion between potential and kinetic energy exemplifies the conservation of mechanical energy, which states that in the absence of non-conservative forces—such as air resistance and friction—the total mechanical energy of the pendulum remains constant. Mathematically, this principle can be illustrated as:
PE_initial + KE_initial = PE_final + KE_final
At the peak, all energy is potential (PE_initial), and at the lowest point, all energy is kinetic (KE_final). Hence, there is an energy transfer but no loss, provided we disregard energy dissipation effects due to external forces.
Nonetheless, in practical scenarios, several factors could disrupt this ideal energy conservation. Air resistance is a prevalent non-conservative force that acts as a damping mechanism. As the bob swings through the air, energy is dissipated as heat; hence, the amplitude gradually decreases over time in a real-world setting. With each oscillation, some energy is lost to the environment, demonstrating that while the principle of energy conservation is upheld in theory, it becomes less apparent in practice where external forces are at play.
Additionally, frictional forces at the pivot point may also contribute to energy loss. The tension in the string, while critical for maintaining circular motion, does not perform work in the system’s energy equation. It merely redirects the force of gravity without contributing to the energy transformation. However, if there is significant friction, the pendulum’s motion can be impeded, leading to further energy dissipation.
Understanding these dynamics of the simple pendulum can have implications in various fields, including engineering and environmental science. For instance, when designing oscillating systems, such as clocks or seismographs, awareness of energy losses and damping effects is crucial for precision and efficiency. In the realm of environmental activism, the principle of energy conservation reflected in pendulum dynamics underscores the importance of minimizing waste and optimizing energy sources. By recognizing conversion efficiencies, greater strides can be made towards sustainable practices.
Moreover, educational contexts benefit immensely from experimenting with a simple pendulum. It serves as an excellent prototype to illustrate fundamental principles of physics and energy conservation to students. Through interactive laboratory experiences, learners can grasp the subtleties of potential and kinetic energy transformation, observing firsthand how energy is conserved under ideal conditions and how external factors can alter that equilibrium. Such systems can cultivate a stronger appreciation for the laws governing motion and energy, fostering an environmental consciousness that recognizes the necessity of conservation efforts in broader environmental contexts.
In conclusion, the simple pendulum offers a profound illustration of the conservation of energy principle. As it intricately transitions between potential and kinetic energy throughout its oscillations, it adheres to the foundational laws of physics. Nevertheless, real-world applications reveal that external forces inevitably disrupt this ideal conservation, emphasizing the pertinence of energy efficiency both in theoretical models and practical applications. Ultimately, understanding such principles not only enhances academic comprehension but equally informs sustainable practices vital to the health of our environment and society.