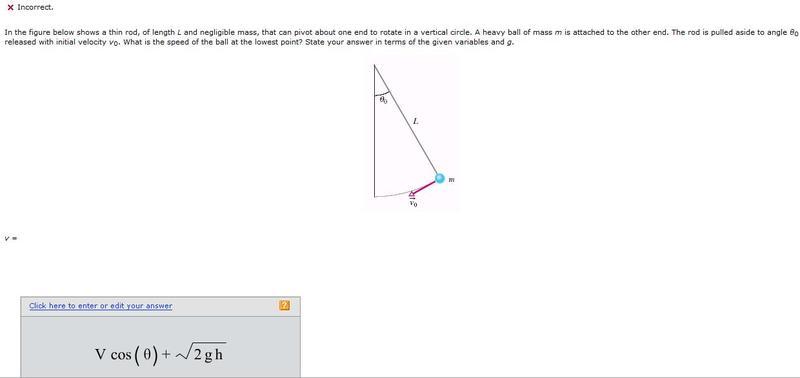
In the realm of classical mechanics, the axiom of energy conservation resonates like a timeless melody, unfurling in a myriad of complexities. At its core, conservation of energy posits that energy cannot be created or destroyed but merely transformed from one form to another. Yet, when we delve deeper into the interplay of kinetic and potential energy, particularly when subjected to varying velocities, a pivotal question arises: is constant velocity requisite for energy conservation? This inquiry beckons us into an intricate dance of physics principles, allowing us to explore the very fabric of motion and energy.
To lay the groundwork, let us evoke the metaphor of a well-tuned orchestra. Each instrument plays its part—a violin shimmering with potential, a percussion drum commanding kinetic force. Together, they create a harmonious symphony. Similarly, in the domain of energy, various forms such as kinetic energy (the energy of motion) and potential energy (stored energy) must interact fluidly. When obstacles disrupt this harmony, as in the case of acceleration or deceleration, one might presume that energy conservation becomes convoluted. However, nature embodies a meticulous design, ensuring that total energy remains constant, irrespective of the velocity.
At first glance, the concept of constant velocity may appear conducive to energy conservation. Uniform motion implies that kinetic energy remains invariant, depicted mathematically by the equation ( KE = frac{1}{2} mv^2 ). Should the velocity be constant, the kinetic energy changes solely with mass alterations. However, the realm of motion is seldom so simple. Imagine a ball rolling down a hill. As it accelerates, kinetic energy increases while potential energy decreases correspondingly. The quickening pace provides an arresting visual of energy transformation, yet both energies maintain a steadfast sum, illustrating that energy can be conserved without adherence to constant velocity.
Consider a practical example: a roller coaster traversing a serpentine track. At the apex of a hill, the coaster harbors maximum potential energy, poised for transformation. As it descends, this potential energy transitions seamlessly into kinetic energy, propelling the car with exhilarating speed. The kinetic energy accrued is not predicated on constant velocity, but instead fluctuates in rhythm with gravitational potential energy. Through various elevations, energy transcends forms without loss, elegantly embodying the principle of conservation.
Nevertheless, the notion of constant velocity possesses its merits, particularly in theoretical discussions and idealized systems. In these scenarios, we encounter Newton’s first law of motion: an object in motion tends to stay in motion with the same speed and in the same direction unless acted upon by a net external force. This concept introduces inertia—an object’s reluctance to change its state of motion—and invites us to contemplate situations devoid of external interference. On a frictionless surface, a projectile hurls onward at a constant velocity, illustrating an isolated system where conservation of kinetic energy can be overtly observed.
The discourse on constant and variable velocities also sheds light on energy dissipation. In real-world systems, external forces—friction, air resistance, and other dissipative forces—inevitably arise. These forces absorb energy and transform it, usually into heat. Thus, while the classical definition of energy conservation holds, the nuances of energy transfer and transformation reveal grander narratives, highlighting intricate interactions between energy forms and their environments. In the grand scheme, energy merely shifts forms, categorized into usable and unusable energy.
Within the microcosm of thermodynamics, the Second Law of Thermodynamics stipulates that potential energy tends to disperse, moving towards states of increased entropy. Exigencies of varied velocities can foster unexpected revelations in energy conservation. For instance, in a closed system, energy transfer across non-constant velocities may yield a cumulative system of energy stasis over time, even as singular components experience fluctuations. This speaks to the dynamic equilibrium that underpins nature’s ability to conserve energy despite motion’s ceaseless ebb and flow.
The convergence of kinetic energy and potential energy ultimately unfurls insights into the very nature of energy itself. As we contemplate constant versus variable velocities, the ever-present truth remains: energy conservation transcends simplicity. The complex relationships interwoven within and beyond the physical entities challenge contours of understanding, illustrating energy as an omnipresent force, ceaselessly reconfiguring itself.
In conclusion, constant velocity is not a prerequisite for the conservation of energy. Rather, it exists as a unique condition within a classical framework that frequently simplifies broader and more intricate realities. Energy requests dynamic interplay, an orchestra that flows, ebbs, and transforms, akin to a river meandering through a landscape. Each moment in this river of energy echoes the principles of conservation, celebrating transformations that unfold irrespective of constant velocities. It is a grand narrative, rich with nuance, illustrating how nature’s choreographed dance of energy proceeds, ensuring that no single form, state, or pace delineates its ultimate continuity.