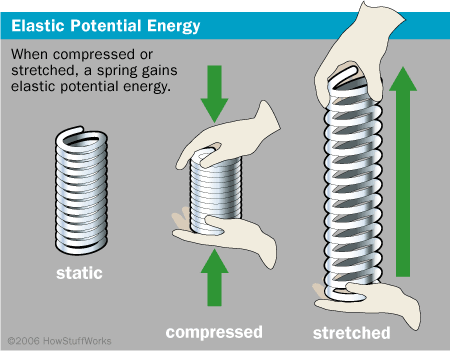
The concept of elastic potential energy is pivotal in understanding the mechanics of forces. More specifically, it pertains to the work done on a material when it is deformed, or in simpler terms, stretched or compressed. A quintessential example lies in the operation of a spring, which stores energy as it is deformed. To explore whether elastic potential energy is a conservative force, it is essential to dissect the characteristics of conservative and non-conservative forces.
At its core, a conservative force is defined as a force that performs work independent of the path taken. It implies that the work done by such a force would be entirely recoverable, depending solely on the initial and final positions of an object within a system. Gravitational and electrostatic forces commonly exemplify conservative forces, as they return energy to the system without losses. This leads us to inquire whether the behavior of elastic forces aligns with these descriptors.
Elastic potential energy manifests when materials such as springs and rubber bands are deformed. The relationship between force and deformation is typically linear as described by Hooke’s Law, which states that the force exerted by a spring is proportional to its displacement. Therefore, the elastic potential energy (EPE) stored in a spring can be mathematically represented by the formula EPE = 1/2 k x², where k is the spring constant and x is the displacement from the equilibrium position.
To evaluate if elastic potential energy qualifies as a conservative force, one must consider the implications of work done on the material. When an elastic material is stretched or compressed, the work done is stored as potential energy accessible for use later. Upon release of the deforming force, the material returns to its original shape, and the stored energy is released. This recovery process is crucial in classifying a force as conservative.
Furthermore, the trajectory of the force’s application is irrelevant in determining the work done by the elastic force. Regardless of how a spring is stretched or compressed, the energy stored when it is deformed stems purely from the displacement and intrinsic properties of the spring material. This reinforces its classification as a conservative force.
Despite the clear indicative traits of elasticity as a conservative force, it is essential to address the real-world applications. Friction, a prevalent non-conservative force, often accompanies elastic systems, leading to energy dissipation. While the elastic potential energy within the spring is recoverable, not all energy can be reclaimed due to losses from friction or internal material resistance. Thus, while the spring itself functions under conservative principles, the entire system may not be exclusively conservative.
In examining the implications of elastic potential energy on engineering and physics, one can identify numerous practical applications. For example, in the design of vehicles, elastic elements in suspension systems optimize shock absorption and enhance comfort. Similarly, in athletic gear, elastic properties in materials contribute to performance efficiency. Each of these applications underscores the utility of elastic potential energy, notwithstanding its behavior in conjunction with external forces.
Moreover, in sports such as gymnastics or trampoline jumping, the concepts of potential energy and kinetic energy interplay intriguingly. The potential energy stored in a compressed springboard translates into kinetic energy, propelling athletes skyward. This integration of energy types is an excellent demonstration of elastic potential energy’s role in performance, revealing the importance of understanding energy conservation principles.
In summation, the classification of elastic potential energy as a conservative force is validated by its fundamental properties. The essence of conservative forces—energy storage recoverability, path independence, and the intrinsic nature of the force—finds an apt example in the behavior of elastic materials. However, one should remain cognizant of the potential interferences posed by non-conservative forces in real-world scenarios.
Understanding elastic potential energy within the realm of conservative forces fosters deeper comprehension of mechanical systems. This understanding not only advances scientific knowledge but also enhances practical applications in technology, engineering, and beyond. Ultimately, recognizing the significance of conserving energy, especially in an era where resource efficiency is paramount, will empower a more sustainable future.