In the realm of classical mechanics, the pendulum serves as a quintessential illustration of energy conservation principles. To comprehend the dynamics of a pendulum’s swing, it is imperative to delve into the interplay of kinetic and potential energy, the defining attributes of mechanical energy, and the concepts of energy transfer and transformation. Central to this discourse is the question: “Is energy conserved in a pendulum’s swing?”
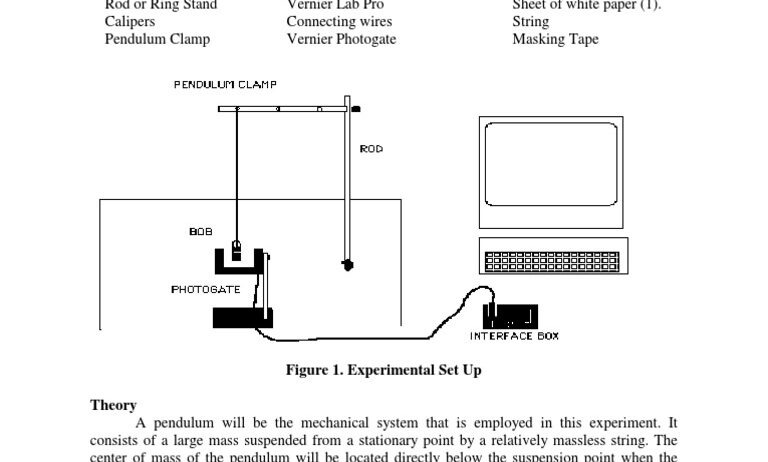
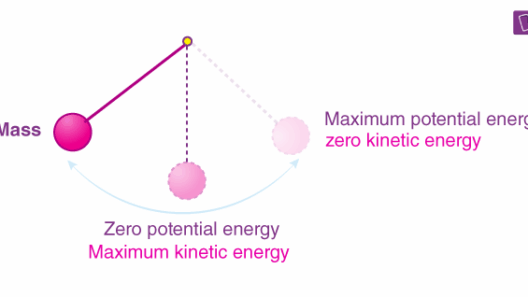
A pendulum consists of a mass (known as the bob) attached to a string or rod, which is anchored at a fixed point. When displaced from its resting position, the bob gains potential energy due to its elevation relative to the lowest point of the swing. This potential energy is denoted by the equation PE = mgh, where PE represents potential energy, m signifies mass, g is the acceleration due to gravity, and h indicates the height above the reference point.
Upon release, this potential energy converts into kinetic energy as the bob descends. Kinetic energy, quantified by the equation KE = 1/2 mv², is dependent on the mass of the bob and its velocity. As the pendulum passes through the lowest point of its arc, the potential energy reaches its minimum, while kinetic energy peaks, illustrating a total mechanical energy balance.
At the pinnacle of its swing, the pendulum momentarily halts before reversing direction, affording a moment to reevaluate energy states. Here, kinetic energy dissipates back into potential energy. This oscillation between potential and kinetic energy encapsulates the core concept of energy conservation within the pendular system.
Throughout its vigorous movements, the pendulum exemplifies a system where mechanical energy is conserved, presuming negligible external forces, such as air resistance or friction. However, theoretical idealization often falls short of real-world applicability. Frictional forces—or energy dissipation mechanisms—would invariably introduce a deviation from true conservation.
The phenomenon of damping significantly influences the conservation of energy in real-world pendulums. Damping is the gradual loss of mechanical energy in a system due to resistive forces like air drag or friction at the pivot point. These forces lead to an exponential decay in the amplitude of oscillation over time. Consequently, while the principles of energy conservation hold in a frictionless environment, real systems exhibit a gradual descent into lower energy states.
Despite such damping effects, certain systems are engineered to sustain energy through various means. For instance, timekeeping pendulums often incorporate devices designed to minimize energy loss, thus prolonging swings. These mechanisms can include carefully polished pivots, altered mass distribution, or magnetic suspensions that counteract damping forces.
Additionally, the context of energy conservation in pendular motion extends beyond mere mechanical principles. One may consider the broader ecological ramifications. Understanding the conservation of energy in a pendulum can serve as an analog for sustainable practices. Just as a pendulum conserves its energy through cyclical transitions, natural ecosystems strive for equilibrium, utilizing resources efficiently to sustain life. The dynamics of energy usage, recycling, and efficient resource management resonate with the oscillatory nature of the pendulum.
To elucidate, consider the application of pendulums in various fields, including engineering and physics education. In educational contexts, pendulums are effective tools for imparting fundamental concepts of energy transformation and mechanical oscillation. Their simple mechanics offers an intuitive glimpse into complex physical principles. Students observe firsthand the transformative capabilities of energy without overwhelming intricacies.
Likewise, engineers leverage pendulum principles in designing structures that withstand oscillations, ensuring stability against environmental forces. Earthquake engineering borrows from these principles to devise systems that absorb and dissipate energy during seismic events, safeguarding human lives and infrastructure. The synergy of pendular motion and energy conservation principles extends far beyond theoretical confines, reaching into practical applications.
Furthermore, the law of conservation of energy also intersects intriguingly with the field of renewable energy. By drawing parallels with pendular motion, one can glean insights into harnessing renewable sources—such as wind or solar power—that recycle energy with minimal waste. Just as a pendulum gracefully harmonizes potential and kinetic energy, sustainable energy systems strive to optimize resource utilization while minimizing environmental impact.
The pendulum, therefore, serves as a profound metaphor for energy conservation, illustrating the duality of transformation and stability. It underscores the necessity of maintaining equilibrium, not just within mechanical systems, but also in broader ecological frameworks. By learning from these oscillatory movements, humans can develop a more holistic approach to conservation, where efficiency and sustainability govern resource use.
Every oscillation reaffirms the fundamental principle—the conservation of energy. Approximately at each extreme, energy transitions occur seamlessly, embodying the very essence of conservation despite real-world complexities that introduce variables. Thus, the pendulum remains a striking representation of how energy can persist and transform, illuminating pathways for sustainable futures through the principles of physics.