As we observe the diverse phenomena in the natural world, one particularly captivating subject arises: the motion of objects in circular trajectories. This motion, so commonplace yet intricately fascinating, invites inquiry into the fundamental principles underpinning our universe. A prevalent question that surfaces in various scientific educational settings is whether energy is conserved in circular motion. The discussion of energy conservation extends beyond the superficial; it delves into the subtleties of dynamics, kinematics, and the principles of classical mechanics, fostering a deeper understanding of spinning bodies in motion.
At the heart of this inquiry lies the law of conservation of energy, stating that energy cannot be created or destroyed, merely transformed from one form to another. This principle applies universally, from the mundane act of a spinning top to the grandiose orbits of planets around the sun. When examining circular motion, we must consider two primary types: uniform and non-uniform circular motion.
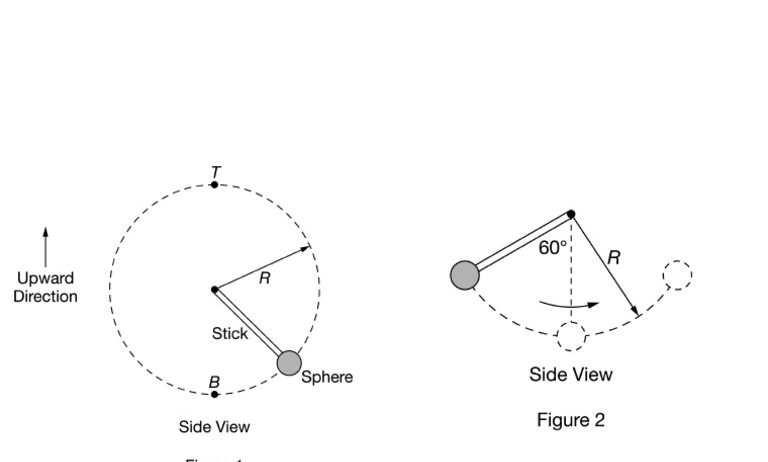
Uniform circular motion occurs when an object moves along a circular path at a constant speed. The forces in play here are intriguing because, at first glance, the kinetic energy of the object seems unaltered. The object’s velocity maintains a constant magnitude; however, this is a simplistic viewpoint. While the speed remains constant, the direction of the velocity vector is continually changing due to the centripetal force acting towards the center of the circle. This force is crucial, as it generates an acceleration that alters the trajectory of the object without changing its speed. In this scenario, the kinetic energy, given by the equation ( KE = frac{1}{2}mv^2 ), remains constant, thus indicating that total mechanical energy is conserved. However, we must not dismiss the energy expenditure related to the force facilitating the circular motion.
As we transition to non-uniform circular motion, the narrative shifts dramatically. In this case, the object experiences a change in speed as it travels along its circular path. The energy transformation is evident here, where kinetic energy fluctuates in correlation to the velocity. As the object speeds up, kinetic energy increases; conversely, as it decelerates, the kinetic energy diminishes. Furthermore, gravitational potential energy can play a pivotal role, particularly when discussing the circular motion of pendulums or celestial bodies. In such cases, energy fluctuates between kinetic and potential forms, yet the total mechanical energy (kinetic plus potential) remains invariant, assuming negligible energy losses due to external factors such as air resistance or friction.
Exploring further, centripetal force is integral in discussing energy conservation in circular motion. This inward-directed force maintains the object’s path. While the object is perpetually undergoing centripetal acceleration, which is an essential component of its circular trajectory, the work done by centripetal force is zero. This introduces a pivotal distinction: while centripetal force is necessary for maintaining the circular path, it does not do work on the object, thereby preserving energy. This interesting characteristic leads to noteworthy discussions regarding the nature of forces and their roles in energy conservation.
Physical phenomena showcase that circular motion embeds more complexities than the elementary aspects of velocity and acceleration. The relation between angular momentum and energy also brings depth to the conversation. Angular momentum (( L )), defined as the product of an object’s moment of inertia (( I )) and its angular velocity (( omega )), remains conserved in isolated systems. This conservation occurs even in circular motion, further amplifying the relationship between rotation and energy. In scenarios devoid of external torques, an object’s angular momentum remains constant, allowing kinetic energy to transform without violating the conservation principles. The transformation crucially highlights how energy circularly traverses within a system.
The enigmatic nature of circular motion also invokes the concept of energy dissipation, presenting avenues for conservation advocates to ponder. In instances where external forces, such as friction or air resistance, become significant, not all energy remains conserved in the mechanical system. Instead, part of the energy transforms into thermal energy, a spillover that often results from non-conservative forces. This transformation leads to inevitable energy loss from the system, challenging the idealized notions of conservation in practical applications. These energy losses often manifest in mechanical systems, thereby prompting engineers and environmentalists alike to seek resolutions through better design adjustments, mitigating losses, and enhancing efficiency.
In the broader context of physics, the principles governing energy conservation in circular motion provide profound insights into various fields, spanning from engineering innovations to ecological implications. Recognizing energy’s fluidity relative to motion can guide sustainable practices aiming to optimize energy usage in mechanical and ecological systems. Although the principles delineated are couched within rigorous mathematics and physics, their ramifications echo into our everyday lives. The energy landscape we navigate, from public transportation to renewable energy systems, turns on these foundational discoveries.
Thus, in addressing the common observation regarding energy conservation in circular motion, we unravel both simplicity and vast complexity. Remarkably engaging, the intertwining threads of mathematics, physics, and the natural world lead to deeper reflections on our environment. Circular motion connects us, enlightening the principles of energy conservation while advocating for efficiency in our modern world. As such, our fascination with spinning bodies encapsulates more than mere observation; it encourages an appreciation for the vibrant, dynamic interplay of forces and energy that not only define our universe but also impact our journey toward sustainability.