Simple Harmonic Motion (SHM) is a fascinating physical phenomenon that many of us encounter in various forms, from pendulums to springs. One might ponder the playful question: Is energy conserved in simple harmonic motion? This inquiry not only invokes curiosity but also leads us to explore the various intricacies of energy dynamics within SHM. As we delve into this topic, we will unravel the underlying principles of energy conservation and its implications in oscillatory systems.
To begin with, it is essential to define what simple harmonic motion actually entails. At its core, SHM is a type of periodic motion characterized by a restoring force that is directly proportional to the displacement from an equilibrium position. This means when an object is displaced, it tends to return to its equilibrium state in a sinusoidal manner. Common examples of SHM include the oscillation of a mass attached to a spring and the swinging of a pendulum.
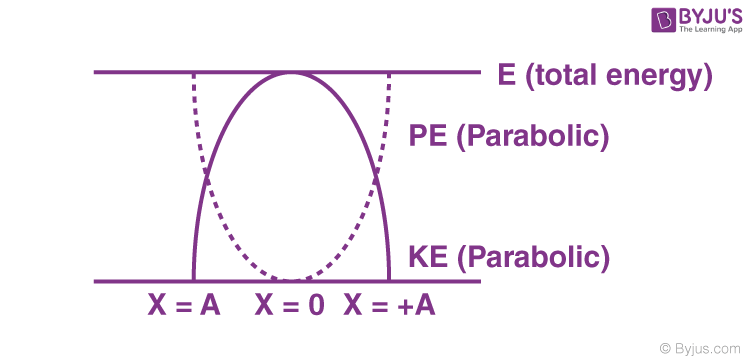
Now, let us consider the fundamental aspect of energy in these oscillatory systems. In SHM, energy oscillates between two forms: kinetic energy (KE) and potential energy (PE). When the object is at the equilibrium position, it possesses maximum kinetic energy and zero potential energy. Conversely, at the maximum displacement points, referred to as the amplitude of the motion, the potential energy reaches its zenith, while kinetic energy becomes nil. This cyclical transformation between KE and PE leads us to the crux of our inquiry—does total mechanical energy remain constant?
Mathematically, this principle can be expressed through the conservation of energy theorem, which states that the total energy of an isolated system remains constant, barring the influence of external forces. In the absence of dampening forces such as friction and air resistance, the net energy will indeed be conserved. Hence, as an object engages in SHM, the sum of kinetic and potential energy remains invariant throughout the oscillation.
However, in real-world applications, external forces are often at play. Friction, air drag, and other forms of resistance can extract energy from the system, leading to a gradual loss of mechanical energy over time. This phenomenon results in damping, which ultimately affects the amplitude and period of oscillation. As the system loses energy, the oscillations become less pronounced until they eventually cease. Thus, one might observe that energy is not conserved in practical terms due to these dissipative forces.
Let us further explore the interplay of forces in SHM. The restoring force, pivotal to SHM, is generally defined through Hooke’s Law, which states that the force exerted by a spring is proportional to the distance it is stretched or compressed from its equilibrium position. Mathematically, this can be represented as F = -kx, where k is the spring constant and x is the displacement. Thus, as a restorative force acts upon the object, it becomes evident that energy conversion occurs seamlessly within the motion’s cycle.
Additionally, it is crucial to consider the impact of mass on energy conservation in SHM. Larger masses result in increased kinetic energy, given the relationship KE = 1/2 mv², where m denotes mass and v stands for velocity. As mass influences the oscillation characteristic and the amount of energy converted, fluctuations in amplitude and period are observed, reiterating that, while energy conversion between forms remains intact, external factors can obstruct conservation.
To illustrate the concept, let’s consider a swinging pendulum. Imagine an ideal scenario where the pendulum is set into motion with no air resistance or friction. It will swing back and forth, transforming potential energy into kinetic energy as it passes through its lowest point. At this juncture, kinetic energy peaks, while potential energy converges to zero. Conversely, when the pendulum reaches its highest point, its kinetic energy becomes negligible while potential energy is maximal. The transformation is systematic, revealing the beauty of energy flow in SHM.
Nevertheless, postulating the question about energy conservation in SHM brings forth philosophical reflections. If we consider a perfectly isolated system void of external influences, energy conservation holds true. Yet, the reality of our physical universe encompasses myriad external forces that impart energy loss. This leads to an essential distinction: theoretical energy conservation versus practical applicability.
Moreover, advancements in technology have introduced innovative applications of SHM, from engineering robust systems like clocks and seismographs to designing energy storage systems based on oscillatory principles. Each application necessitates a keen understanding of energy exchange, emphasizing the significance of recognizing both the theoretical and practical implications of energy conservation in SHM.
In summary, the intriguing world of simple harmonic motion offers profound insights into the conservation of energy. While energy transformation between kinetic and potential forms is conserved in an ideal environment, the reality of frictional and external forces complicates this phenomenon. The exploration of energy dynamics in SHM not only fuels our curiosity but also empowers us to rethink our approach to energy conservation in a broader context. Thus, we are left to ponder: how can we apply these principles of energy management to foster sustainability in our everyday lives and transform energy usage for future generations?