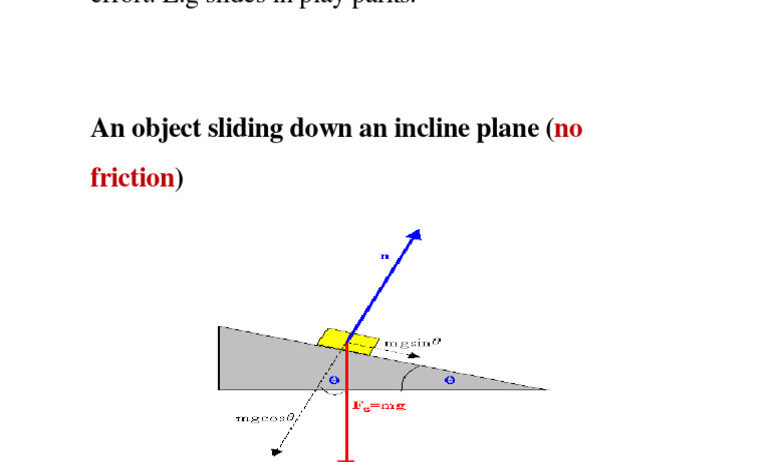
When pondering the principles of physics, one may wonder: is energy conserved on an incline plane? This seemingly simple question leads us down a path rich with complexity and nuance. The inquiry not only challenges our understanding of energy transfer and conservation but also serves as an illustrative example of fundamental principles in mechanics.
To begin addressing this query, it is essential to delineate the key components involved in an incline plane. An incline plane, or inclined plane, is a flat surface that is tilted at an angle to the horizontal. This setup is frequently employed in physics experiments to understand the dynamics of forces and motion. The classic example is the ramp; whether it’s a skateboard ramp or a construction site ramp used for moving heavy materials, it demonstrates how gravity interacts with inclined surfaces.
At first glance, one might assume that energy is always conserved. After all, the law of conservation of energy posits that energy cannot be created or destroyed; it can only transform from one form to another. However, in the context of an incline plane, the situation becomes more intricate. A key factor to consider is gravitational potential energy (GPE) and kinetic energy (KE).
When an object is placed at a height above the ground on an incline, it possesses gravitational potential energy determined by the formula: GPE = mgh, where m is mass, g is the acceleration due to gravity, and h is the height. As this object descends the incline, its height diminishes, leading to a corresponding decrease in gravitational potential energy. Simultaneously, there is a transformation of this potential energy into kinetic energy, described by the formula: KE = 1/2 mv², where v represents the velocity of the object.
As the object rolls or slides down the incline, the conversion of energy takes place. The total mechanical energy of the system (i.e., the sum of GPE and KE) remains constant, provided that no opposing forces act upon it. This notion of total mechanical energy conservation is contingent upon the absence of friction and air resistance, which can convert mechanical energy into thermal energy, thereby dissipating it.
However, in practical scenarios, such as with a real-world incline, some energy is invariably lost to friction. The force of friction is an omnipresent antagonist, constantly working against the motion of objects on inclined surfaces. This frictional force does work on the object, converting some mechanical energy into heat. The result is that the total mechanical energy is not conserved; instead, it is reduced by the work done against friction.
So, what happens to energy on an incline? When an object glides down an incline, we observe the intricate interplay between GPE, KE, and dissipative forces. Energy is transformed rather than lost entirely, but some of it is rendered unusable for mechanical work due to dissipation through non-conservative forces. This phenomenon introduces an intriguing aspect to our question: Does this mean energy is not conserved? The answer lies in the understanding that while mechanical energy is not conserved in the presence of external forces, the total energy of the system continues to obey the conservation laws in a broader sense, encompassing all forms of energy including thermal energy.
One might further question: How does the angle of the incline affect energy conservation? The degree of inclination modifies the distribution between potential and kinetic energy. A steeper incline will yield a greater conversion rate from GPE to KE, resulting in a faster-moving object at the base of the incline. Conversely, a gentler slope results in a more gradual transformation, thus prolonging the duration of energy transfer and the interaction with dissipative forces.
Moreover, the intrinsic nature of the materials involved plays a pivotal role. Different surfaces, characterized by varying coefficients of friction, will influence the extent of energy dissipation. For instance, a wooden plank versus a metal ramp will yield disparate results in terms of energy conservation outcomes, due to their distinct frictional properties. The choice of material not only impacts efficiency but also has real-world implications, particularly in engineering design and energy efficiency pursuits.
In consideration of all these factors, the inquiry into whether energy is conserved on an incline plane transforms into a more multifaceted exploration of physical principles governing motion and energy transformation. Therefore, during the descent down the incline, the energy is neither created nor annihilated. Instead, it transitions between forms—potential to kinetic—while some fraction may be irretrievably lost to the environment as heat due to friction.
Ultimately, the original question regarding the conservation of energy on an incline plane may now be viewed through a lens that appreciates both the conservation laws and the practical effects of friction and material properties. This complex interplay encapsulates the beauty of physics: challenges often become profound learning experiences. We are reminded that while energy conservation is a fundamental concept, the reality of its application can vary significantly according to specific conditions. Thus, energy is conserved in a grand sense—the transformation is continuous, and the investigation into these principles enriches our understanding of the physical world around us.