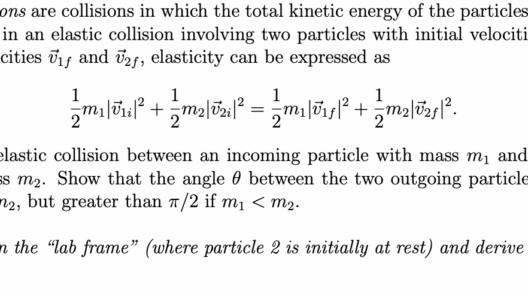Kinetic energy, a term encountered frequently in the realms of physics, refers to the energy possessed by an object due to its motion. Defined mathematically, kinetic energy (KE) can be expressed as KE = 1/2 mv², where ‘m’ represents mass and ‘v’ stands for velocity. The concept of kinetic energy conservation is pivotal in understanding various physical systems, yet it is essential to delineate the conditions under which kinetic energy is conserved and those in which it is not.
To grasp kinetic energy conservation, it is imperative to consider the principle of conservation of energy, which asserts that energy cannot be created or destroyed but can only be transformed from one form to another. Consequently, while mechanical energy may exhibit conservation in certain scenarios, kinetic energy is a specific form of mechanical energy that demonstrates varying conservation properties based on the nature of the interactions involved.
To develop a deeper understanding, this discourse explores the contexts in which kinetic energy remains conserved, the scenarios in which it dissipates, and the underlying mechanisms affecting its conservation.
Conditions Favoring Conservation of Kinetic Energy
In elastic collisions, kinetic energy is conserved. An elastic collision occurs when two objects collide and rebound without permanent deformation or generation of heat. During such interactions, both momentum and kinetic energy are conserved. A quintessential example is the collision of two ideal billiard balls on a frictionless table. Upon colliding, they swap velocities while maintaining their total kinetic energy, demonstrating a fundamental principle of elastic interactions.
Additionally, systems devoid of external forces or frictional influences also showcase conservation of kinetic energy. In an ideal vacuum, where no energy loss occurs to friction or air resistance, a sliding object continues to maintain its kinetic energy until it encounters an unbalanced external force. This phenomenon aligns well within the confines of Newtonian mechanics, underscoring the importance of isolated systems in kinetic energy preservation.
Mathematical Implications of Conservation
The mathematical representation of momentum conservation in elastic collisions provides an insightful analytical tool. When two bodies collide elastically, the conservation laws can be articulated as follows:
P_initial = P_final (for momentum)
KE_initial = KE_final (for kinetic energy)
In scenarios where these equations hold true, one can confidently assert that kinetic energy is conserved, signifying an unaltered energy state throughout the collision process.
Situations of Kinetic Energy Dissipation
Contrarily, in inelastic collisions, kinetic energy is not conserved. An inelastic collision entails a scenario where colliding bodies experience deformation, resulting in the conversion of kinetic energy into other energy forms—such as sound, heat, or internal energy. Classic examples of inelastic interactions include car crashes, where some kinetic energy is transformed into sound, heat, and structural deformation. The aftermath of such collisions often illustrates palpable losses in kinetic energy and transformation into work done against friction and other forces.
Furthermore, when dealing with frictional forces, kinetic energy is invariably converted into thermal energy. The shoes sliding on a pavement generate heat due to friction, dissipating kinetic energy. In such cases, it becomes evident that despite the work done on the surface, kinetic energy is irretrievably lost in the form of frictional heating.
The Role of External Forces
Analyzing the impact of external forces unveils an additional layer to the concept of kinetic energy conservation. An external force alters the energy distribution within a system. When an external force—such as gravity, friction, or electromagnetic forces—acts on a body, it can induce changes in kinetic energy levels. For example, an object rolling down an inclined plane experiences an increase in kinetic energy as gravitational potential energy is converted. The transformation highlights not only the interplay of different energy forms but also the significance of external factors in governing energy behavior.
The Conceptual Spectrum of Energy Conservation
Considering kinetic energy on a broader conceptual spectrum, energy conservation encompasses a range of interactions beyond mere collisions. For instance, in rotational dynamics, angular kinetic energy manifests similarly to translational kinetic energy. Systems exhibiting rigid body motion adhere to conservation principles under specific conditions, thus extending the discussion of kinetic energy conservation to rotational frameworks.
Final Thoughts on Kinetic Energy Conservation
The dichotomy of kinetic energy conservation fundamentally hinges on the nature of interactions among bodies, external influences, and the type of collision involved. While elastic collisions uphold the tenets of energy conservation, inelastic collisions and the presence of external forces illustrate scenarios where kinetic energy dissipates into alternate forms. Understanding these conditions fosters a clearer comprehension of kinetic energy mechanics, thus empowering individuals to predict energy behavior across diverse physical phenomena.
In conclusion, kinetic energy is not universally conserved—it is contingent on the contexts of interactions. As we engage with the world, recognizing how energy transfer and transformation play out in our daily experiences enhances our grasp of fundamental physical principles, paving the way for informed decision-making in various scientific and engineering endeavors.