Kinetic energy is a principle rooted deeply in the laws of physics and can be best understood through the lens of a closed system. In such a system, energy, in the form of kinetic energy, can behave in ways that illuminate fundamental principles of conservation and transformation. To unravel these concepts, we must first comprehend the mechanics of energy conservation and the types of collisions that can occur in a closed system.
In classical mechanics, a closed system is defined as one that does not exchange matter or energy with its surroundings. Within this system, the total energy remains constant—a fundamental postulate of the law of conservation of energy. This means that while energy can change forms (e.g., from kinetic to potential energy), the total amount of energy within the closed system remains invariant.
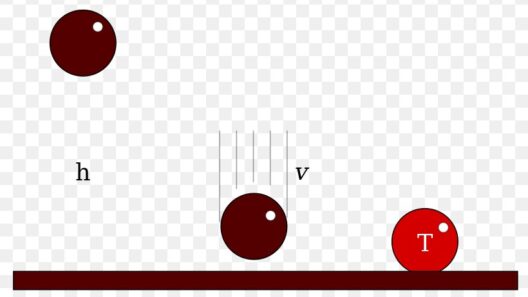
Kinetic energy, characterized by the equation K.E. = 1/2 mv² (where m represents mass and v is velocity), is the energy associated with the motion of an object. When discussing conservation within closed systems, it is essential to consider different types of collisions that can occur: elastic and inelastic collisions. The nature of these collisions dictates the behavior of kinetic energy and momentum.
In an elastic collision, both kinetic energy and momentum are conserved. This occurs when two colliding bodies rebound off each other without any loss of kinetic energy in the process. A quintessential example of an elastic collision can be observed in the interaction between two billiard balls. The moment the balls collide, they transfer energy between them in such a manner that the total kinetic energy before and after the collision remains unchanged. This illustrates the core tenet of conservation—energy is simply redistributed, not lost.
Conversely, inelastic collisions present a different scenario. While momentum still remains conserved in these collisions, kinetic energy is not. A classic example is the collision of two cars in a crash. Upon impact, the vehicles crumple, and their deformation is indicative of energy being transformed into sound, heat, or internal energy rather than remaining in the kinetic form. Thus, while the total momentum of the system remains constant, the overall kinetic energy diminishes, highlighting the transformation of energy rather than its conservation in the kinetic sense.
Nevertheless, it is crucial to elucidate that although kinetic energy is not conserved in inelastic collisions, the law of conservation of energy still applies to the entire system. The energy has not vanished; it has simply transitioned into different forms, such as thermal energy or potential energy due to deformation. This nuanced understanding reiterates that energy conservation encompasses all forms of energy, thereby preserving the overall integrity of the closed system.
In practice, energy within a closed system can be subjected to various influences, including external forces. Although these forces may introduce complications, in purely theoretical physics, closed systems are often considered in isolation. This simplification permits a clearer analysis of energy transformations during dynamic processes.
A critical consideration is the role of friction and air resistance. While these forces do exert influence on real-world applications, they often complicate the simplistic view of closed systems. In idealized scenarios where such forces are negligible, the laws of kinetic energy conservation can be easily demonstrated. However, in realistic conditions, energy losses typically occur, which are crucial for understanding systems like machinery and vehicles that rely on kinetic energy for operation.
Furthermore, beyond simply adhering to conservation laws, the implications of kinetic energy conservation in closed systems extend into practical realms, such as engineering, astrophysics, and even recreational activities like sports. When designing vehicles, engineers must consider energy transformations to ensure safety and efficiency. Similarly, understanding kinetic energy can enhance athletic performance by optimizing techniques to maximize energy use during activities such as running or swimming.
A historical context also significantly enriches our comprehension of kinetic energy. The inception of kinetic theory laid the groundwork for modern physics. Pioneers such as Galileo and Newton made substantial contributions to understanding motion and energy. Their principles remain bedrocks upon which further explorations into the microscopic realms of particle physics and thermodynamics are built. As science progresses, these fundamental concepts facilitate a bridge to complex phenomena like chaos theory and quantum mechanics.
In an ecological context, the conservation of energy principles also resonate beyond the confines of physics. In ecosystems, energy transfer through trophic levels showcases the transformation of energy rather than loss. From sunlight to photosynthesis, energy flows as organisms convert it into various usable forms, mirroring the principles of energy conservation observed in physical systems.
In conclusion, while the question persists: is kinetic energy conserved in a closed system? The answer encapsulates a more profound understanding of energy, movement, and transformation. In elastic collisions, kinetic energy is preserved, while in inelastic collisions, the energy morphs into other forms, reaffirming that energy cannot be created or destroyed. This wealth of understanding enhances our grasp of the physical universe, providing a foundation that is crucial for both theoretical inquiry and practical applications across various fields. Endeavors to explore these principles further can lead to innovative solutions to energy challenges facing contemporary society, advocating for both conservation and efficient utilization. The exploration of kinetic energy will undoubtedly remain a pivotal point of our ongoing quest for knowledge.