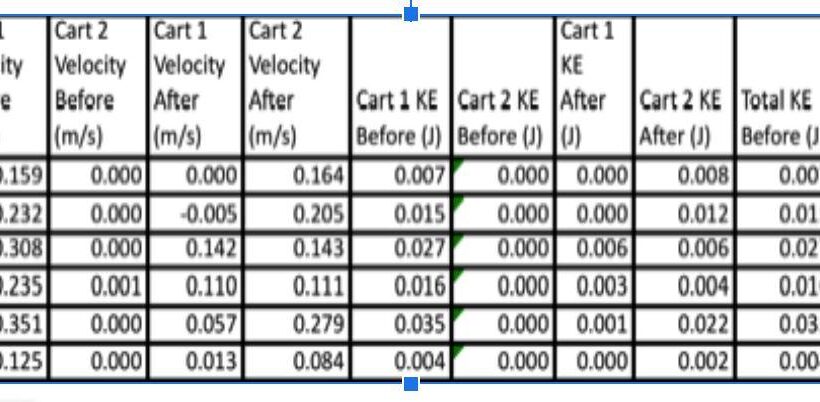
Understanding the principles of energy conservation is pivotal to grasping various phenomena in physics, and the specific case of kinetic energy in magnetic bumper collisions provides a fascinating arena for exploration. At the intersection of electromagnetism and classical mechanics, questions arise: Is kinetic energy conserved during interactions involving magnetic fields, and what implications does this have for our understanding of energy transfer? This inquiry invites a deeper examination.
First, it is essential to clarify the foundational tenets of kinetic energy. Kinetic energy, a form of mechanical energy, is defined as the energy an object possesses due to its motion. It is quantified through the formula K.E. = 1/2 mv², where m represents mass and v is velocity. In classical physics, the law of conservation of energy asserts that in a closed system, the total energy remains constant, merely transforming from one form to another during interactions.
Magnetic bumper collisions take place when two or more objects interact within magnetic fields, often utilized in experimental setups or engineering applications to analyze momentum and energy transfer. Unlike elastic or inelastic collisions, where energy conservation laws apply differently, magnetic interactions introduce unique variables. In essence, these interactions exemplify how energy might be redistributed rather than strictly conserved in its kinetic form.
A pivotal aspect to consider is the nature of the collision. In elastic collisions, kinetic energy before and after the event remains invariant, provided that no external forces do work on the system. Contrarily, in inelastic collisions, some kinetic energy transforms into other energy types, such as thermal energy, rendering it unavailable for mechanical work. Magnetic bumper collisions often exhibit characteristics of inelasticity, given that some kinetic energy is converted into magnetic potential energy and other forms during the interaction.
Moreover, the role of magnetic fields in these collisions adds layers of complexity. When two objects with magnetic properties collide, their kinetic energies can be affected by the dynamics of attraction and repulsion dictated by their magnetic fields. For instance, as two magnets approach each other, they accelerate due to the magnetic attractive force. Upon collision, the magnetic force counteracts the initial kinetic energy, diverting it into different energy states.
This transformation highlights a critical principle: while kinetic energy may not be preserved in its totality during these magnetic interactions, the overall energy of the system remains conserved when accounting for all energy forms. Therefore, the question of conservation of kinetic energy in magnetic collisions challenges the classical interpretation by showcasing how energy can transition between various forms while upholding the broader conservation principle.
As these principles unfold, one can ponder the implications of magnetic bumper collisions in advanced technological applications. For instance, in the design of magnetic levitation (maglev) systems, understanding the transfer and conservation of energy during motion is paramount. Maglev trains utilize magnetic fields for propulsion, and during their operations, the conservation of total energy—encompassing electromagnetic, kinetic, and thermal components—lies at the forefront of engineering designs. Consequently, a thorough understanding of magnetic collisions equips engineers and physicists with the knowledge to optimize these systems for efficiency and performance.
Additionally, examining kinetic energy conservation in magnetic bumper collisions encourages further inquiry into potential innovations. Could this understanding open doors to novel methods of energy storage and transfer? Could we harness these magnetic interactions in ways that enhance sustainability and environmental consciousness? Addressing these queries not only piques scientific curiosity but also aligns with a larger dialogue on energy efficiency and the potential to mitigate environmental impacts.
In summary, while magnetic bumper collisions do not conserve kinetic energy in the classical sense, they illuminate critical principles of energy transformation. The distinctions between elastic and inelastic collisions become especially pronounced, prompting a reevaluation of our assumptions regarding kinetic energy. Notably, understanding the nuances of these collisions sheds light on broader phenomena within physics and far-reaching implications for technology. As we navigate the intersection of energy conservation and technological innovation, the pursuit of knowledge in this area remains an essential endeavor.
Ultimately, exploring whether kinetic energy is conserved in magnetic bumper collisions goes beyond theoretical speculation. It embarks on a journey into the heart of physics, demanding an appreciation for the complexities of energy interactions. As researchers and engineers continue to delve into this realm, they promise not only a shift in perspective but also the potential for transformative advancements in a world that increasingly seeks sustainable solutions.