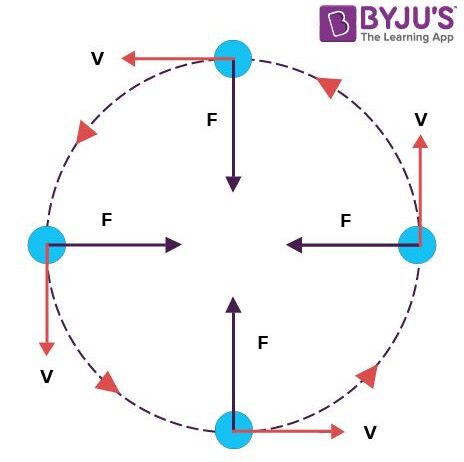
Uniform circular motion (UCM) describes the motion of an object that moves in a circular path at a constant speed. This means that while the speed remains unchanged, the velocity is not constant because the direction is continuously changing. A crucial aspect of physics is understanding the energies involved in such a motion, particularly kinetic energy. The question often arises: Is kinetic energy conserved in uniform circular motion? To adequately answer this, we must delve into both the mechanics of UCM and the principles of energy conservation.
Understanding Kinetic Energy
Kinetic energy (KE) is defined as the energy that an object possesses due to its motion, quantitatively represented by the formula KE = ½ mv², where m is the mass of the object and v is its speed. In the context of uniform circular motion, an object moves in a circle and maintains a constant speed, which implies that both its mass and speed remain unchanged throughout the motion. Nonetheless, the direction of motion continuously varies.
The Nature of Uniform Circular Motion
When analyzing uniform circular motion, it is pivotal to acknowledge the role of centripetal force. This inward force is necessary to maintain circular motion and acts perpendicular to the direction of the object’s instantaneous velocity. While one might initially think that uniform motion implies a consistent energy state, the changing direction indicates otherwise. However, since the speed remains constant, the kinetic energy of the object in UCM does not vary.
This aspect leads to the critical realization that while position and velocity direction are dynamic in UCM, the kinetic energy remains a constant value as long as no external net work is conducted on the object. Thus, in ideal conditions devoid of friction or other dissipative forces, kinetic energy remains conserved.
Conditions for Conservation of Kinetic Energy
In the context of mechanical energy conservation, it’s paramount to consider various influences that might disrupt the conservation of kinetic energy. For example, introducing friction or air resistance leads to energy dissipation, primarily converting kinetic energy into thermal energy. Therefore, kinetic energy in UCM is only conserved under ideal conditions where external forces do not influence the system.
Potential Energy Considerations
In addition to kinetic energy, potential energy plays a significant role in circular motion scenarios. While moving in a vertical circular path, an object experiences variations in gravitational potential energy. For instance, at the top of the circular path, potential energy is at its maximum, while at the bottom, it reaches its minimum. As the object moves along this path, energy transforms between kinetic and potential forms.
The interplay between kinetic and potential energy in such situations reflects the law of conservation of mechanical energy, which states that the total mechanical energy (kinetic plus potential) of an object remains constant when only conservative forces act upon it. This principle emphasizes that in scenarios of vertical circular motion, kinetic energy is not strictly conserved; it fluctuates due to gravitational influence, while the overall mechanical energy remains conserved.
Kinetic Energy in Non-Ideal Conditions
In real-world applications, uniform circular motion rarely remains unencumbered by external influences. Friction, drag, and other forms of resistance invariably alter the kinetic energy of moving objects. For instance, a car navigating a circular road must exert continuous force overcoming friction to maintain its path, resulting in a net loss of kinetic energy transformed into heat. Moreover, tires also deform and recover energy, further complicating the energy dynamics in UCM contexts.
Furthermore, if we consider an object undergoing circular motion while experiencing rotational forces, the energy analytics become even more intricate. Torque and angular momentum must then be factored into energetic assessments, recognizing their impact on both the kinetic and overall energy dynamics at play.
Practical Implications of Kinetic Energy in UCM
Understanding kinetic energy in uniform circular motion has far-reaching implications, especially in engineering and various technological applications. For example, designing amusement park rides requires precise calculations of energy to ensure safety and longevity. Knowledge of how kinetic energy behaves in UCM is also pivotal in fields like vehicular design, astronaut training, and even in analyzing planetary orbits.
Moreover, in sports mechanics, athletes often apply principles of UCM to enhance performance, whether through track racing, swimming, or gymnastics. Insights into kinetic energy conservation allow for more efficient energy usage, ultimately leading to improved results and reduced risk of injury.
Conclusion
In conclusion, kinetic energy in uniform circular motion demonstrates unique characteristics significant to comprehending energy conservation principles. While kinetic energy remains conserved under ideal conditions of UCM, it oscillates in systems influenced by gravitational potential energy or non-conservative forces. This delicate balance of energies—kinetic, potential, and the external forces acting thereupon—provides a comprehensive understanding of motion in circular paths. Recognizing the nuances inherent in these interactions is crucial for applications spanning scientific research to practical engineering challenges.