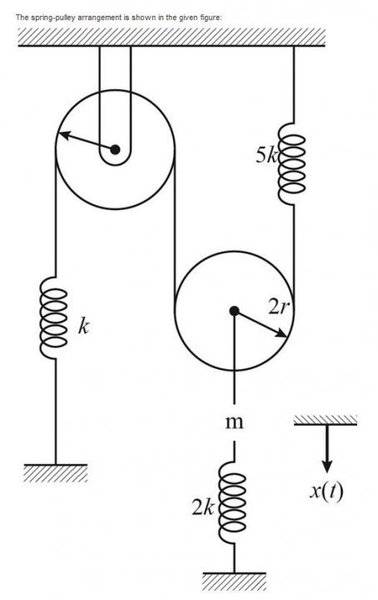
The concept of mechanical energy conservation is pivotal in classical mechanics, presenting a fascinating intersection of motion, force, and energy dynamics. To elucidate whether mechanical energy is conserved between two distinct points, A and B, it is crucial to dissect the fundamental principles governing mechanical energy and the conditions under which it remains conserved.
Mechanical energy is the sum of kinetic energy (the energy of motion) and potential energy (energy stored due to an object’s position). Mathematically, it can be expressed as:
Mechanical Energy (ME) = Kinetic Energy (KE) + Potential Energy (PE)
Kinetic energy is defined as:
KE = 1/2 mv²
where m is mass and v is velocity. Potential energy, often in a gravitational context, can be expressed as:
PE = mgh
where m is mass, g is the acceleration due to gravity, and h is the height above a reference point. The interplay of these energy forms delineates whether energy is conserved during motion between two defined points.
In an ideal system, where only conservative forces are at play—such as gravitational or elastic forces—a fundamental tenet of physics asserts that the total mechanical energy remains consistent throughout the motion from point A to point B. This principle rests on the premise that there are no external forces or energy losses, such as friction or air resistance, acting on the system. This conservation of mechanical energy can be summarized by the equation:
ME_A = ME_B
Thus, the total mechanical energy at point A equals the total mechanical energy at point B. If the kinetic energy at point A is high due to a considerable velocity and low height, one might see a transformation of that energy into potential energy as the object elevates to point B, thus slowing down. In this scenario, energy shifts form but the total remains constant, showcasing the beauty of energy transformation.
However, mechanical energy conservation does not hold in all scenarios. The introduction of non-conservative forces—such as friction, air resistance, or any form of dissipation—alters this elegant balance. For example, consider a block sliding down a friction-laden ramp. As the block descends, some of its potential energy is converted into kinetic energy, yet additional energy is expended overcoming frictional forces, resulting in a loss of total mechanical energy from the system. Here, mechanical energy cannot be considered conserved, as energy has been irretrievably converted into thermal energy and other forms during the interaction with the surface of the ramp.
To delve deeper into our energy conservation inquiry between points A and B, one must also consider the nature of the motion involved. If the system is influenced by external forces—like an applied force or alterations in the mass of the object—the energy equations must be recalibrated to reflect these interactions. The presence of external work done on the system modifies total mechanical energy, thus necessitating an alteration in the conservation equation:
ME_A + Work = ME_B
This equation underscores the complexity inherent in real-world systems as mechanical energy relies heavily on the interplay of various forces acting upon a body. The manifestation of these forces can lead to a myriad of fascinating phenomena, each revealing the nuanced behavior of energy in motion.
Another compelling aspect of this inquiry is the principle of energy transformations in oscillatory systems, such as pendulums or springs. These systems elegantly illustrate conservation principles as they oscillate between kinetic and potential states. As a pendulum swings from its highest point (maximum potential energy) to its lowest point (maximum kinetic energy), mechanical energy remains conserved, showcasing the intricate dance of forces in play.
It is also worth noting the implications of energy conservation principles beyond mere academic curiosity. Understanding the behavior of mechanical energy has vast applications in fields such as engineering, renewable energy design, and environmental conservation. By maximizing efficiency and minimizing energy losses, we can devise mechanisms and structures that operate sustainably, ensuring a balance in energy use that aligns with ecological considerations.
However, the conservation of mechanical energy is not an absolute, immutable rule. It serves as a model for understanding ideal conditions while recognizing the influence of real-world complications. This awareness fosters innovation as we strive to create systems that honor the principles of conservation while adapting to the intricacies of dynamic interactions with the environment.
In conclusion, whether mechanical energy is conserved between points A and B hinges on several crucial factors, including the nature of the forces at play, the type of system under consideration, and the conditions imposed on that system. This exploration unveils a world where energy transitions, transformations, and conservation reign, revealing the astounding intricacies of our physical universe. Through persistent inquiry and a commitment to understanding these principles, we unveil the deeper parallels between energy conservation in mechanics and broader environmental stewardship, binding our pursuits of knowledge to the realities of sustainable practices.