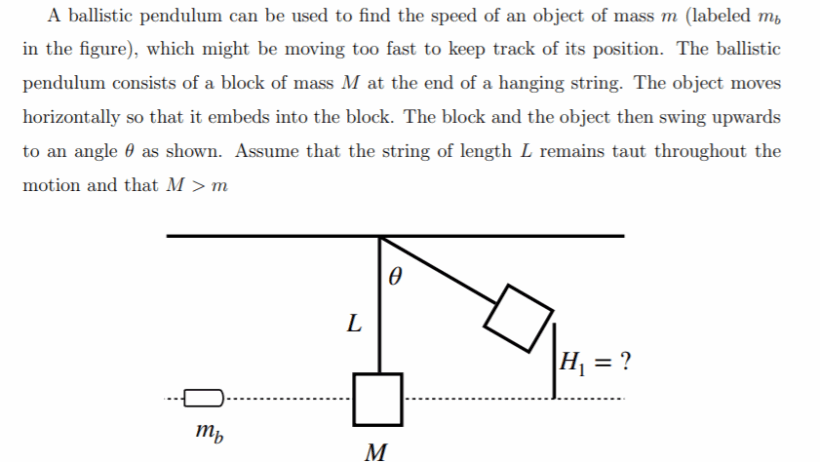
The ballistic pendulum is a fascinating apparatus that elegantly demonstrates principles of physics related to momentum and energy conservation. Central to the discussion of the ballistic pendulum is the consideration of mechanical energy conservation during the interaction of the projectile and the pendulum. This inquiry into energy conservation is crucial for understanding numerous phenomena across various fields, including engineering, sports physics, and ballistic design.
To scrutinize whether mechanical energy is conserved in a ballistic pendulum, one must first understand the components involved. A ballistic pendulum typically consists of a pendulum bob—a weight suspended from a pivot—and a projectile which strikes the pendulum bob. Upon collision, the projectile embeds itself within the pendulum, resulting in a single system that moves together after the interaction. Analyzing the energy transformations that occur during this interaction requires a fundamental understanding of kinetic and potential energy.
Mechanical energy is defined as the sum of kinetic energy (the energy associated with motion) and potential energy (the energy stored due to an object’s position in a gravitational field). Prior to the collision, the projectile possesses kinetic energy as it travels and the pendulum bob remains stationary, thus containing no kinetic or potential energy relative to its lowest point. The initial mechanical energy of the system is exclusively attributed to the moving projectile. However, once the projectile collides with the bob and becomes lodged within it, the system’s dynamics change drastically.
At the moment of impact, the conservation of momentum principle comes into play. This principle states that in the absence of external forces, the total momentum before the collision must be equal to the total momentum after the collision. Mathematically, this is represented as:
M1V1 + M2V2 = (M1 + M2)Vf
In this equation, M1 represents the mass of the projectile, V1 its velocity before impact, M2 the mass of the pendulum bob, V2 its initial velocity (which is zero), and Vf the final velocity of the combined system (projectile plus pendulum) immediately after the collision.
A significant takeaway from this analysis is that although momentum is conserved, mechanical energy is not conserved during the impact due to the inelastic nature of the collision. Inelastic collisions result in the conversion of some kinetic energy into other forms of energy, such as thermal energy and energy associated with sound. During the impact, deformation occurs, both in the projectile and the pendulum, indicating that not all initial kinetic energy transforms into kinetic energy of the system post-collision.
After the projectile embeds itself into the pendulum bob, the mechanical energy transformation undergoes further examination. The pendulum begins to swing upward, converting kinetic energy (at the moment of collision) into potential energy (as it rises to its peak height). The maximum height achieved by the pendulum illustrates a key point of interest. At its zenith, the pendulum momentarily ceases moving, illustrating that the kinetic energy has been completely converted into potential energy at this point. This potential energy is determined by the height reached and can be expressed with the equation:
PE = mgh
Where ‘m’ is the mass of the bobsled system, ‘g’ is the acceleration due to gravity, and ‘h’ is the height reached. At this peak, the pendulum’s mechanical energy is conserved in the form of potential energy. However, it’s prudent to note that the total mechanical energy of the system—considering the mechanical energy before the impact—has diminished due to the inelastic nature of the collision.
An elucidation of this concept is paramount: mechanical energy is temporarily conserved in the form of total energy within the pendulum system after impact, but the initial state (the sum of potential and kinetic energy) when the projectile was moving is not equal to the final state post-collision. The discrepancy arises due to energy loss resulting from the inelastic collision.
As the pendulum swings back down, it converts potential energy back to kinetic energy, clearly demonstrating the conservation of energy within the system. However, series loss mechanisms such as air resistance and internal deformations during the collision continuously detract from the total energy available for conversion. These factors create an inefficiency which is observable in practical experiments based on real-world conditions.
In summation, the inquiry into whether mechanical energy is conserved in a ballistic pendulum establishes two critical conclusions. Firstly, momentum conservation holds true throughout the collision, allowing for predictive calculations of velocities pre- and post-impact. Secondly, mechanical energy is not conserved during the impact but is conserved in the form of potential energy during the pendulum’s subsequent motion. The elegance of the ballistic pendulum lies not only in its illustrative capacity regarding core physics concepts but also showcases the intricate dance of energy transformations, reminding us of the fundamental laws that govern motion and energy in our universe.
The ballistic pendulum exemplifies the complexities of energy exchange and the importance of understanding mechanical interactions, serving as a critical educational platform for aspiring physicists and engineers. Its implications extend far beyond that of academic curiosity, affecting real-world applications, and reminding us of the intricacies involved in energy conservation.