When exploring the dynamics of physical systems, one may often stumble upon the principle of mechanical energy conservation. However, the question remains: is mechanical energy genuinely conserved during a collision? To dissect this conundrum, one must delve into the intricacies of mechanical energy, the nature of collisions, and the overarching physical laws that govern these phenomena.
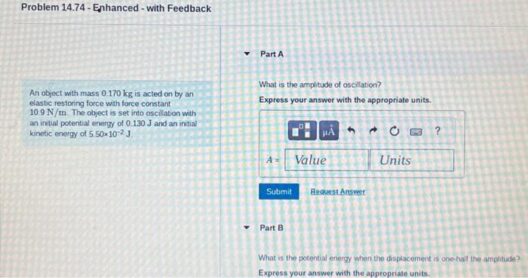
Mechanical energy is categorized into two primary components: kinetic energy (the energy of motion) and potential energy (the stored energy due to position). The law of conservation of mechanical energy states that in an isolated system with no external forces, the total mechanical energy remains constant. This principle holds true primarily in ideal conditions, where factors such as friction, air resistance, and other dissipative forces are negligible. In these scenarios, mechanical energy is effectively conserved.
However, collisions introduce complexities into the conservation discussion. Collisions can be broadly classified into two categories: elastic and inelastic collisions. In elastic collisions, both momentum and kinetic energy are conserved. These types of collisions occur in idealized scenarios, such as the interactions between gas molecules or perfectly hard spheres in a vacuum. The total kinetic energy before and after an elastic collision remains invariant, making it a clear example where mechanical energy conservation holds.
On the contrary, inelastic collisions present a different narrative. These are events where momentum is conserved, yet kinetic energy is not. A quintessential example of an inelastic collision is the crash of two automobiles. Although the total momentum of the system (the combined mass times the velocity of both vehicles) remains unchanged, a substantial portion of kinetic energy is transformed into other forms of energy, such as sound, heat, and deformation energy within the vehicles. This results in a tangible loss of mechanical energy, thereby challenging the conservation theorem.
Moreover, the degree of inelasticity is not uniform across all collisions. Some collisions are perfectly inelastic, where the involved bodies stick together post-collision, and kinetic energy reaches a minimum. In these extreme cases, the loss of kinetic energy can be substantial. In contrast, other inelastic interactions may permit some kinetic energy retention, although it still does not conform to the conservation law as dictated by perfectly elastic criteria.
To understand the implications of mechanical energy conservation in collisions, consider the conservation of momentum. The momentum of a system is preserved when no external forces interfere, regardless of whether the collision is elastic or inelastic. This reinforces the idea that, while kinetic energy may transform or dissipate, motion (momentum) continues in a predictable manner. This relationship illustrates that momentum is a more robust quantity for analyzing collisions, particularly in real-world applications.
Furthermore, the real-world application of these principles extends to various fields including automotive safety design, sports science, and even astrophysics. Engineers employ the principles of momentum and energy conservation to design crumple zones in vehicles that absorb and redistribute energy during collisions, minimizing the impact on passengers. Likewise, athletes leverage knowledge of kinetic energy to optimize performance through technique adjustments based on momentum dynamics.
When evaluating the conservation of mechanical energy in collisions, it is also essential to consider external factors. In practical scenarios, frictional forces, air resistance, and even sound generation play pivotal roles in energy dissipation. Consequently, while the idealized models might clearly define conservation in a vacuum, real-world applications necessitate a broader analysis that acknowledges the energy lost to non-mechanical forms.
While energy conservation laws remain fundamental, the nuances surrounding mechanical energy in collisions underscore the necessity of contextual understanding. Illustrated through various types of collisions, it becomes evident that while momentum persists, energy transformations necessitate reevaluation of mechanical energy conservation principles. Each type of collision serves as a case study, elucidating the interplay between kinetic and potential energies, and further highlighting the implications for conservation in practical applications.
Ultimately, the complex interplay of mechanical energy during collisions invites further inquiry and analysis. Whether through the lens of theoretical physics or pragmatic engineering solutions, comprehending mechanical energy dynamics equips us with profound insights into the natural world. From the tiniest particles colliding in a gas to the monumental forces at play in car accidents, the preservation of energy—be it through conservation, transformation, or dissipation—remains a vital yet intricate aspect of physics worthy of exploration.