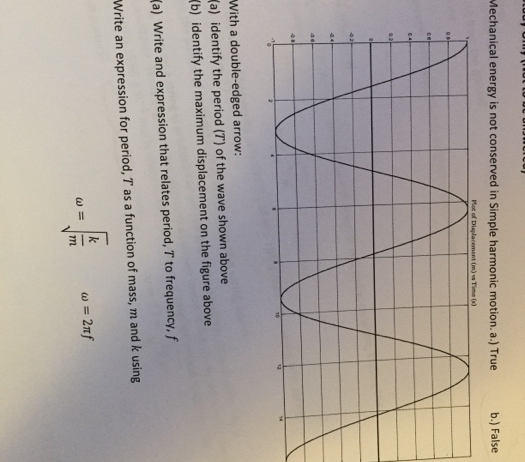
In the realm of physics, the conservation of mechanical energy is a pivotal concept, particularly when investigating Simple Harmonic Motion (SHM). The fundamental question arises: is mechanical energy conserved in SHM? This topic encompasses various dimensions of physics, including energy transformations, force interactions, and oscillatory motion, collectively contributing to a comprehensive understanding of SHM.
To delve into this subject, it is first essential to clarify what is encapsulated within mechanical energy. Mechanical energy is the sum of potential energy (PE) and kinetic energy (KE) within a system. Potential energy is stored energy based on an object’s position, while kinetic energy is the energy of motion, defined by the velocity and mass of the object. In the context of SHM, potential and kinetic energy interconvert as an object oscillates around an equilibrium position.
Simple Harmonic Motion is characterized by periodic oscillations. A classic example of SHM is the motion of a mass attached to a spring. When the mass is displaced from its equilibrium position, the spring exerts a restoring force, propelling the mass back toward equilibrium in a sinusoidal pattern. This periodic nature of the motion allows for an intricate interplay between kinetic and potential energy.
In an ideal system devoid of any external forces or dissipative effects, the total mechanical energy remains constant. Such conditions represent a theoretical framework wherein energy transformations occur seamlessly—kinetic energy at its maximum when the mass is at the equilibrium position and potential energy at its maximum when the mass reaches the extremes of its motion. At these extreme points, the kinetic energy is minimal (zero), as the mass momentarily comes to rest before reversing direction. Conversely, when the object is at its equilibrium position, the potential energy is at a minimum, leading to a peak in kinetic energy. This cyclical transformation corroborates the principle of conservation of mechanical energy in SHM.
However, in real-world applications, systems often experience energy losses due to non-conservative forces such as friction or air resistance. These forces dissipate energy, often transforming it into thermal energy, thus leading to a gradual decrease in the total mechanical energy of the system. For instance, consider a pendulum in a dampened environment; over time, the pendulum will gradually lose amplitude until it eventually comes to rest. This phenomenon showcases how external influences can disrupt the conservation of mechanical energy.
The mathematical description of SHM is governed by a second-order differential equation, which encapsulates the restoring force’s dependence on displacement. This relationship illuminates why energy conservation in SHM is often sine wave-like. The position of the mass can be represented as a function of time, where displacement is proportional to the sine function. This sinusoidal motion inherently supports the narrative of energy transformation between potential and kinetic states.
Examining potential energy specifically, we note that for a mass-spring system, the potential energy ( PE ) can be mathematically expressed as ( PE = frac{1}{2}kx^2 ), where ( k ) is the spring constant and ( x ) is the displacement from equilibrium. Similarly, the kinetic energy ( KE ) is articulated as ( KE = frac{1}{2}mv^2 ), where ( m ) is the mass and ( v ) is the velocity of the mass. By examining these equations, one can confirm that at various positions during the oscillation, the total mechanical energy ( E ) remains constant in an ideal scenario: ( E = PE + KE ).
In corporate and industrial applications, the principles of SHM and energy conservation are crucial for the design of resonating systems, such as tuning forks or oscillators in electronic circuits. Accurately predicting energy conservation helps engineers design systems that maximize efficiency and minimize waste. This optimization is critical not just for efficiency but also for ecological considerations, enhancing sustainability by reducing energy consumption.
It’s fundamental also to consider the implications of energy conservation laws in education. Teaching students about SHM reinforces foundational physics concepts while fostering analytical thinking. Experiments with pendulums or springs serve to visually demonstrate energy transformation, making theoretical principles tangible. Engaging students with real-life applications evokes a deeper appreciation for the laws governing motion and energy.
Furthermore, the philosophical reflections surrounding conservation laws invite profound inquiries into the nature of energy itself. Questions arise about the universe’s fundamental properties and the implications of energy dissipation. In a broader sense, this conversation intersects with contemporary discussions on sustainability and energy efficiency; understanding mechanical energy conservation informs methods of reducing energy waste in various systems.
In conclusion, while mechanical energy in an idealized setting of Simple Harmonic Motion is conserved perpetually through the interplay of kinetic and potential energies, real-world scenarios often introduce variables that disrupt this conservation. A thorough understanding of these concepts enhances not only academic inquiry within physics but also practical applications across numerous disciplines, laying a groundwork for innovation and sustainability. Realizing energy conservation in SHM is not merely a theoretical exercise but is vital for producing sustainable solutions in a world increasingly focused on efficient resource utilization.