When analyzing mechanical systems, particularly those exhibiting oscillatory motion, we arrive at an intriguing question: Is mechanical energy conserved in underdamped oscillators? This query delves into the fundamentals of classical mechanics, engaging students and enthusiasts alike. Understanding this phenomenon involves unraveling the complexities of energy conservation laws, damping mechanisms, and the nature of oscillatory systems.
To grasp the argument surrounding mechanical energy conservation, we first need to establish a foundation in oscillatory motion. In simple harmonic motion (SHM), objects oscillate about an equilibrium position. They experience a restoring force proportional to their displacement, leading to sinusoidal motion. In an ideal system devoid of any resistive forces—such as friction or air resistance—mechanical energy remains constant throughout the oscillation. However, real-world systems often display damping, which can significantly alter the energy dynamics.
Underdamped oscillators are a particular category of oscillatory systems where damping is present but is not strong enough to prevent oscillations altogether. These systems continue to oscillate while gradually losing energy over time due to damping forces. The classic example of an underdamped system is a mass-spring system where the mass, when displaced, will not only return to its equilibrium position but will also overshoot, taking time to settle down to this position.
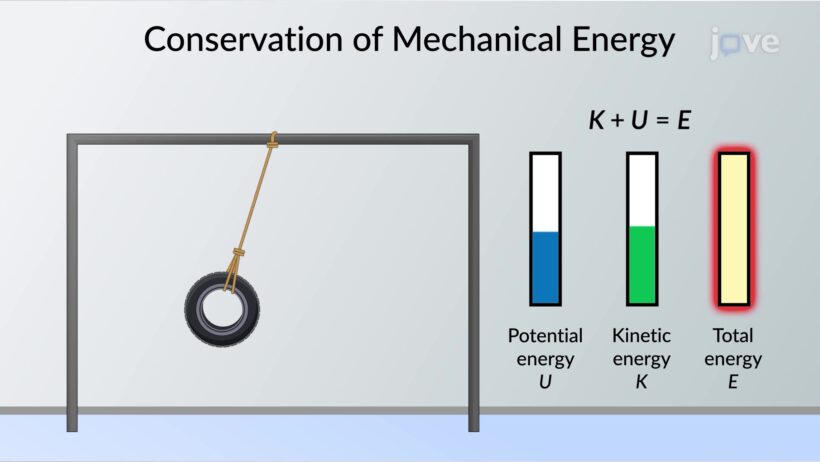
In underdamped oscillators, mechanical energy can be expressed as the sum of potential and kinetic energy. During oscillation, energy transforms back and forth between these two forms. At maximum displacement, potential energy is at its peak while kinetic energy is minimal. Conversely, at the equilibrium position, potential energy reaches its lowest point, and kinetic energy peaks. The total mechanical energy, in the absence of damping, remains constant throughout this process.
However, introducing damping leads us to a salient point: mechanical energy is not conserved in underdamped oscillators. As a result of damping forces, likely arising from friction or other resistive factors, energy is dissipated in the form of heat or sound. Each oscillation results in a gradual reduction of energy. This leads to a characteristic amplitude decay over time, which can be described mathematically using exponential decay functions.
One must now consider why this phenomenon occurs and its implications in various fields. The fascination with underdamped oscillators stems from their prevalence in everyday life, where they can be observed in numerous applications—from car suspensions to musical instruments. The behavior of these oscillators can have profound effects, making them crucial for engineers and designers who seek to optimize performance while minimizing energy loss.
The degree of damping largely determines the oscillator’s behavior. Underdamped systems experience oscillations with a gradually diminishing amplitude, which creates a visual representation of how energy dissipates over time, raising questions about efficiency and sustainability. As energy conservation becomes a paramount consideration in our modern world, understanding these oscillators allows scientists and environmentalists to develop more efficient systems, whether that is through improved materials, shapes, or designs that reduce friction.
The analysis of energy conservation in underdamped oscillators also raises philosophical questions about the nature of energy itself. While mechanical energy is not conserved, it transforms into other forms. This presents an opportunity to explore energy’s role in different contexts. For instance, the kinetic energy lost in an underdamped system manifests as thermal energy, which, in certain applications, could be harnessed for practical usage. Novel technologies that harness waste energy are on the rise, revealing potential for increased efficiency even within systems considered inefficient by design.
Another critical point is the role of resonance in underdamped systems. When external forces match the natural frequency of the oscillator, resonance can occur, leading to dramatic increases in amplitude. This phenomenon showcases the delicate balance between energy input and dissipation. Engineers must understand this to prevent structural failures in bridges or buildings, where underdamped oscillations triggered by environmental forces can result in catastrophic outcomes.
To encapsulate the entire discussion, it is essential to underscore the principle that in underdamped oscillators, mechanical energy is not conserved due to the influence of damping forces. While energy transformation occurs through oscillatory motion, the gradual dissipation of energy serves as a reminder of the inefficiencies oftentimes present in our systems. Observing this energy behavior not only enhances our comprehension of mechanical principles but serves as a crucial guide in engineering and environmental conservation efforts.
Ultimately, the investigation into underdamped oscillators highlights the interplay between theory and application. It encourages a deeper understanding of the complexities of energy dynamics, nurturing a sense of responsibility to design and innovate with energy conservation in mind. As the world grapples with energy challenges, the knowledge of underdamped oscillators provides an important framework that may inform future advancements and sustainable practices.