The phenomenon of standing waves is a captivating study within the realms of physics. They manifest themselves in various physical systems, from musical instruments to vibrating strings and even in the context of waves on strings suspended between two points. However, this begs the question: is mechanical energy conserved in the context of a standing wave? To address this inquiry, one must embark on a journey through the principles of wave mechanics, energy transformations, and conservation laws governing physical systems.
To initiate this discussion, let’s ponder a playful question—what occurs to the mechanical energy when a standing wave is established? At first glance, standing waves may seem to retain their energy, constantly oscillating in a cyclical pattern. However, upon closer examination, the intriguing interplay of energy transformation unveils a more complex picture. The conservation of mechanical energy in the context of standing waves necessitates an understanding of its constituent components: kinetic and potential energy.
Mechanical energy is predominantly characterized by two forms: kinetic energy, associated with motion, and potential energy, which offers a measure of stored energy in a system based on position or configuration. In a standing wave, these two forms are inextricably linked, oscillating in tandem as energy transitions between kinetic and potential forms throughout the wave cycle.
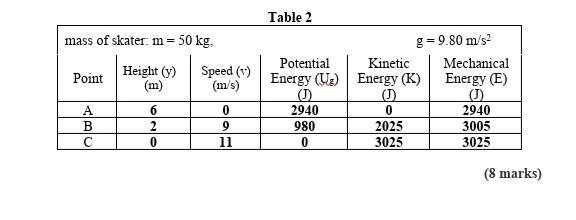
In a vibrating string, for example, when the string reaches its maximum displacement from the equilibrium position (often referred to as the amplitude of the wave), it possesses maximum potential energy. Here, the kinetic energy is minimal since the particles of the string momentarily come to rest before reversing direction. Conversely, as the wave traverses toward the equilibrium position, the potential energy diminishes as the kinetic energy surges, peaking at the equilibrium point where the motion of the string’s particles is at its most energetic. This oscillation between forms exemplifies the conservation of mechanical energy in a closed system absent external forces.
But does this situation hold true for the entirety of the standing wave phenomenon? In an idealized model characterized by a perfect system devoid of dissipative forces, one might argue that yes, mechanical energy is conserved. However, reality often introduces complexities that challenge this assertion. In tangible systems, factors such as friction, air resistance, or internal damping effects contribute to energy dissipation, leading to a gradual decrease of mechanical energy in the system over time.
Let’s consider the implications of these energy losses. When damping is present, mechanical energy is transformed into other forms, predominantly thermal energy. This energy conversion occurs through frictional forces that oppose the motion of the particles. Hence, the energy originally present in the vibrating system progressively diminishes, and as a result, the mechanical energy is not conserved. This brings to light an essential consideration: the broader environmental context in which these waves exist.
The dramatic implications of energy conservation laws extend into the environmental realm as well. If one were to apply these principles to the analysis of musical instruments, for example, it invites a fascinating inquiry into efficiency. The amount of energy expended in sound production illuminates inefficiencies and prompts discussions about optimizing design for a more sustainable future. Understanding energy transformation within the context of standing waves provides invaluable insights into enhancing the efficient use of resources.
Additionally, one must consider the influence of boundary conditions on standing wave behavior. When confined between two fixed points, standing waves can demonstrate varying characteristics depending on their physical setting, which influences the associated energy profiles. Nodes and antinodes—points of no displacement and maximum displacement, respectively—exemplify the distinct energy distribution inherent in standing waves. Analyzing how these points interact with one another reveals critical aspects of energy conservation and dissipation in real-world applications.
As one delves deeper into the study of mechanical energy within standing waves, it becomes apparent that the concept transcends mere academic interest. It raises pertinent questions about design efficiency, energy capture, and the sustainability of technological applications reliant on wave principles. The careful consideration of energy conservation principles can guide innovations that harness vibrational energy in a manner that maximizes output while minimizing waste.
In summary, the exploration of mechanical energy conservation in the context of standing waves is multifaceted. While, in a theoretical and idealized framework, one could assert that mechanical energy is conserved, the realities dictated by our physical world demonstrate that factors such as damping can lead to energy loss. This interaction not only reinforces the principles of energy conservation but also opens avenues for enhancing efficiency in real-world applications. Ultimately, navigating the complexities of these systems fosters a heightened awareness of the energetic dynamics at play and invites ideas that may lead to sustainable practices in the future.
Perhaps as you engage with this discussion, a challenge lies before you—what innovative methods might you conceive to harness the energy of standing waves effectively? How can we integrate this understanding into our broader strategies for conservation and sustainability? The answers may reveal themselves as physics meets practicality in our quest for efficient energy utilization.