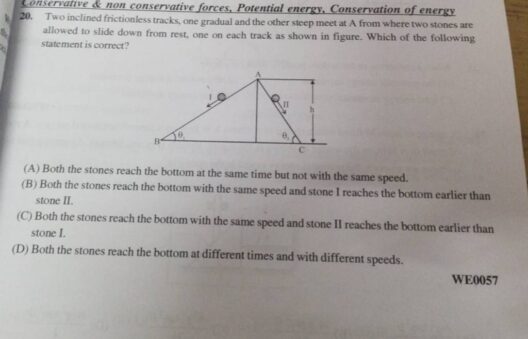
When delving into the realms of physics and energy, one stumbles upon a captivating question: “Is mechanical energy conserved when a conservative force does work?” To dissect this inquiry, it is crucial to understand the foundational elements involved—namely mechanical energy and conservative forces. The exploration of these concepts unravels a tapestry woven with intricate threads of physics that govern the natural world.
Mechanical energy, a fundamental quantity in classical mechanics, is the sum of kinetic energy (the energy of motion) and potential energy (the stored energy due to position). This duality can be likened to a harmonious duet, where kinetic energy and potential energy dance gracefully through the corridors of motion and position. On the other hand, conservative forces, quintessential from the vantage point of energy conservation, are forces that perform work irrespective of the path taken. Examples include gravitational force and elastic spring force. Each of these forces bears the extraordinary ability to return energy back to the system—hence the conservation enigma.
Consider the analogy of a mountain and a playful child sliding down its slope. The gravitational force acting on the child serves as a conservative force. When the child starts at the top, perched precariously at the pinnacle, potential energy is at its zenith; it is poised for an exhilarating descent. As the child slides downward, potential energy relinquishes its grasp while kinetic energy burgeons. At the bottom, gravitational force has done work upon the child; however, the total mechanical energy remains constant throughout the journey. In essence, the child’s adventure down the hill illustrates mechanical energy conservation in action, epitomizing how the potential transforms seamlessly into kinetic, all while the work done by gravity remains true to its conservative nature.
The remarkable property of conservative forces lies in their path independence—work done by a conservative force depends solely on the initial and final states of the system, not the journey it undertakes. This characteristic paves the way for mechanical energy to be conserved in scenarios where conservative forces are at play. The elegance of the principle is embodied in the work-energy theorem, which states that the work done on an object is equal to the change in kinetic energy. Thus, if a conservative force is the agent of work, the mechanical energies before and after the interaction must balance each other out, like a meticulously curated budget that never strays into deficit.
However, it is essential to acknowledge the boundaries of this conservation principle. The domain of conservative forces does not frivolously extend to non-conservative forces—friction, air resistance, and tension, to name a few. These forces exuberantly dissipate energy, transforming mechanical energy into thermal energy, thus resulting in a shortfall of the mechanical balance. Picture a ship sailing on a serene lake; while the wind propels the craft forward, the hidden currents and tides can quietly sap the ship’s potential, illustrating the stark contrast between the nurturing embrace of conservative forces and the relentless grip of non-conservative ones.
The analysis deepens further when addressing scenarios involving mechanical energy conservation in isolated systems. In an optimal context, where only conservative forces exert influence, one can convene a remarkable conclusion: the mechanical energy remains invariant. However, observe this situation in the real world; while the laws of physics remain unwavering, the complexities encapsulated by surrounding environments often conspire against perfect conservation. For instance, consider a pendulum swinging through an arc. While the gravitational pull acts conservatively to maintain energy equilibrium, air resistance and friction at the pivot ultimately draw energy away from the system, leading to a gradual loss of mechanical energy over time.
Hence, it becomes crucial to delineate the variables at play. Beyond the simplistic perspective of energy conservation, the intricate mechanics often result in fascinating phenomena. Take the case of energy transformations. When a conservative force does work, one can observe energy morphing from potential to kinetic and vice versa. This metamorphosis echoes the cycles of nature, where energy is neither created nor destroyed but merely transformed into different states—a principle famously articulated by the first law of thermodynamics.
In practical terms, the applications and implications of mechanical energy conservation pulse through various sectors, from engineering to environmental science. Engineers harness these principles to design efficient machines that encapsulate energy with minimal loss. From renewable energy systems to the construction of roller coasters, understanding mechanical energy conservation is paramount to innovation. In environmental contexts, recognizing energy losses prompts initiatives aimed at reducing waste and maximizing efficiency—an endeavor that underscores our communal responsibility towards sustainable practices.
In conclusion, the question of whether mechanical energy is conserved when a conservative force does work unveils an extensive and intricate landscape. Through an examination of conservative forces, kinetic and potential energies, and the nuanced entities of non-conservative forces, one gleans insight into the conservative nature of energy within defined systems. While the philosophical and practical dimensions of energy conservation appear deceptively simple, they echo a profound truth about the world: energy is an intricate tapestry of motion, transformation, and balance, and as stewards of this planet, understanding and preserving these principles is paramount for a sustainable future.