In the realm of classical mechanics, a pertinent inquiry arises: is mechanical energy conserved when angular momentum is conserved? To address this question, we must delve into the intricate relationship between angular momentum and mechanical energy, and examine their conservation laws in various systems. Understanding these concepts not only enlightens us about the fundamental principles of physics but also enhances our comprehension of real-world phenomena encountered in engineering, astrophysics, and even daily life.
To begin, it is imperative to define mechanical energy and angular momentum. Mechanical energy encapsulates the sum of kinetic and potential energy within a physical system. Kinetic energy is associated with the motion of an object, while potential energy pertains to its position or configuration. Conversely, angular momentum represents the rotational equivalent of linear momentum, serving as a measure of an object’s rotational inertia and its velocity around a particular axis. Mathematically, angular momentum (L) is expressed as the product of rotational inertia (I) and angular velocity (ω): L = Iω.
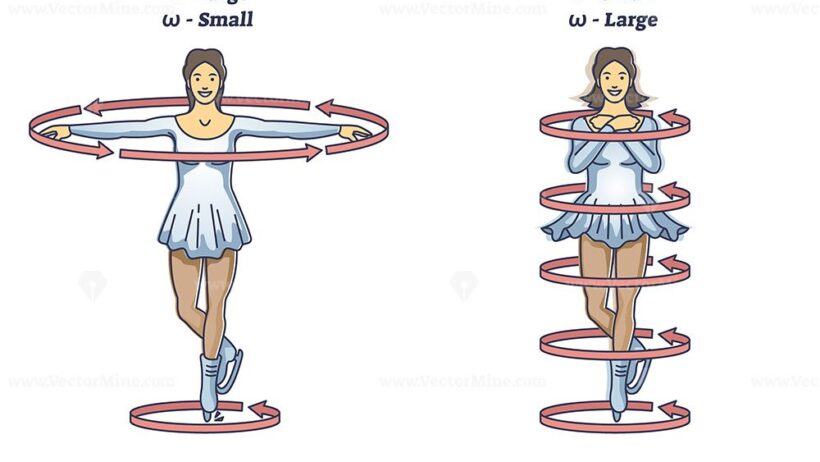
The conservation of angular momentum states that in an isolated system—where no external torques are acting—the total angular momentum remains constant. This principle is incredibly significant, particularly in scenarios where objects are free to rotate. For instance, consider a figure skater executing a spin. As the skater pulls her arms closer to her body, she reduces her moment of inertia. To maintain angular momentum, her rotational speed increases, allowing her to spin faster without the application of any external torque. This illustrates a clear example of angular momentum conservation in action.
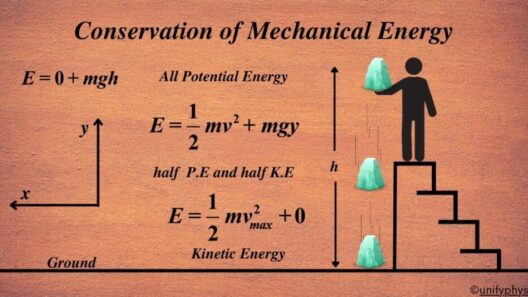
Mechanical energy conservation, on the other hand, hinges on the absence of non-conservative forces. In an ideal system devoid of friction or air resistance, the total mechanical energy remains constant. However, the introduction of external forces, such as friction, dissipates energy, leading to non-conservation of mechanical energy. An everyday example encompasses a pendulum swinging in a frictionless environment; while the potential energy is converted to kinetic energy and vice versa, the total mechanical energy stays unchanged.
Now, juxtaposing these two conservation laws invites contemplation of their interrelationship. When one observes a system where angular momentum is conserved, one may initially be inclined to reason that mechanical energy must also be conserved. However, this is not universally true. The conservation of angular momentum does not inherently imply conservation of mechanical energy. A notable case to consider is a inelastic collision involving rotating bodies. In such collisions, angular momentum may remain unchanged, but kinetic energy is not conserved. This discrepancy arises from the transformation of kinetic energy into other forms, such as heat or sound, through inelastic interactions.
Another illustrative example may be found in the dynamics of a spinning top. As the top spins, its angular momentum is conserved due to the lack of external torques. Nevertheless, the mechanical energy can fluctuate. If the top is spinning on a surface with friction, some of its kinetic energy dissipates as thermal energy due to frictional forces acting upon it. Hence, while the angular momentum is preserved, the mechanical energy is gradually reduced. This underscores a vital principle: the conservation of angular momentum does not require the conservation of mechanical energy.
As we navigate through more complex systems, this relationship becomes further nuanced. In celestial mechanics, for instance, consider a planet orbiting around a star. The angular momentum of the planet with respect to the star remains constant as it travels along its orbital path, yet the mechanical energy may vary due to gravitational interactions and changes in orbital shape. Under some circumstances, gravitational potential energy transforms into kinetic energy as the planet accelerates through periapsis, the point of closest approach to the star. Thus, the conservation of angular momentum persists while mechanical energy famously oscillates.
The intimate connection between these conservation laws prompts a deeper exploration of physical systems. Understanding when and why mechanical energy is conserved or not brings to light critical implications for myriad applications. Engineers exploit these principles to create efficient machines, astronomers use them to analyze celestial behavior, while physicists seek to unify our understanding of physical laws under various conditions. All of these endeavors build upon the tapestry of conservation laws and the insight they provide into natural phenomena.
In synopsis, the conservation of angular momentum and mechanical energy, while occasionally conflated, represent distinct principles with their own particular conditions and implications. The conservation of angular momentum does not guarantee mechanical energy conservation. Various factors, including the type of interaction, presence of external forces, and conditions of friction, play pivotal roles in determining energy dynamics within a system. This intricate interplay between angular momentum and mechanical energy embodies much of the fascination inherent in classical mechanics—an understanding that underlies the entire world of physics and its many applications in our everyday lives.