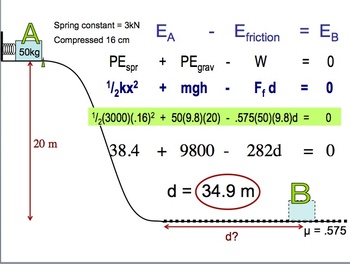
Mechanical energy is a fundamental concept in physics, encompassing both kinetic energy (energy of motion) and potential energy (stored energy due to an object’s position). The law of conservation of mechanical energy states that in an isolated system, where no external forces act upon the objects, the total mechanical energy remains constant. However, the real-world conditions often deviate from the ideal scenarios typically described in theoretical discussions. Hence, the question arises: is mechanical energy truly conserved in real-world conditions?
To address this question, it’s imperative to first understand the conditions under which mechanical energy is conserved. In a perfectly isolated system devoid of any non-conservative forces — like friction or air resistance — mechanical energy would remain constant throughout various interactions and transformations. For instance, a pendulum swinging through its arc ideally converts potential energy at its peak height into kinetic energy at its minimum height. In such an ideal scenario, mechanical energy conservation seems unequivocally applicable.
However, the real world is replete with dissipative forces that fundamentally alter this ideal. Take, for example, a swinging pendulum, where air resistance and internal friction in the pivot reduce the mechanical energy of the system over time. Each swing will reach a lower height than the previous one due to energy conversion into thermal energy, thereby illustrating how mechanical energy is not conserved in this instance. The introduction of non-conservative forces invariably leads to a dissipation of mechanical energy, emphasizing how real-world dynamics differ from theoretical models.
In mechanical systems, energy conversion is also pivotal. Consider roller coasters, which are quintessential examples of converting potential energy into kinetic energy and vice versa. While climbing to the peak, potential energy surges as kinetic energy wanes. However, the moment the coaster begins its descent, and throughout its journey, various forms of energy loss occur, including sound energy (from rattling tracks) and thermal energy (from friction between the wheels and the tracks). Each of these energy transformations signifies that while mechanical energy may be continually exchanged within the system, it is not wholly conserved due to energy dissipation.
Moreover, when analyzing mechanical energy conservation, one must also consider the conservation of energy in broader contexts. For instance, when examining systems involving collisions, such as billiard balls striking each other, mechanical energy may not be fully conserved due to partial inelasticity in collisions. Inelastic collisions result in some kinetic energy converting into other energy forms, such as sound or deformation energy, further compromising the apparent conservation of mechanical energy.
Another pertinent example is the phenomenon of rolling motion, where rotational kinetic energy transcends the complexity of straightforward translational motion. In a rolling object, both translational and rotational kinetic energy contribute to the overall mechanical energy. However, factors like frictional forces act to dissipate energy. Rolling without slipping incurs energy losses, which lead to a non-conservation of mechanical energy even in scenarios that may appear straightforward upon initial observation.
The implications of understanding mechanical energy conservation are far-reaching across various engineering and environmental domains. For instance, innovations in renewable energy technologies, such as wind turbines or hydroelectric dams, hinge upon efficiently harnessing energy conversions. Recognizing that mechanical energy is subject to losses necessitates the development of systems that augment energy efficiency. Engineers must design with an acute awareness of real-world conditions to influence the performance of structures and machinery critically.
Furthermore, the principles of mechanical energy conservation extend to ecological considerations. Ecosystems thrive on energy exchanges and conversions as primary producers, like plants, convert solar energy into chemical energy through photosynthesis. The efficiency with which energy is transformed can directly affect the overall health and sustainability of ecological systems. Biodiversity within ecosystems ensures that energy flows optimally through food webs. The acknowledgment of energy conservation principles emphasizes the importance of preserving our natural environments to maintain these delicate balances.
In conclusion, while the law of conservation of mechanical energy serves as a cornerstone principle in physics, its applicability in real-world scenarios is often compromised by various dissipative forces and non-conservative interactions. Mechanical energy is not entirely conserved due to the ubiquitous presence of friction, air resistance, and energy transformations that occur during dynamical processes. Recognizing these nuances is essential for advancing engineering practices and understanding ecological interdependencies. Thus, the quest for sustainable practices and efficient designs must consider the inevitable dissipation of mechanical energy while striving to minimize energy losses in systems, extending our capability to harness energy effectively while respecting natural laws.