The Moon’s orbit around the Earth is one of the most visually captivating phenomena in the night sky. As observers on Earth, we frequently notice its phases, its distance, and its gravitational dance with our planet. This leads to a fundamental question: Is the Moon’s orbit an example of mechanical energy conservation? To address this, it is crucial to unpack the concept of mechanical energy, examine the dynamics of celestial bodies, and explore the laws of physics that govern these interactions.
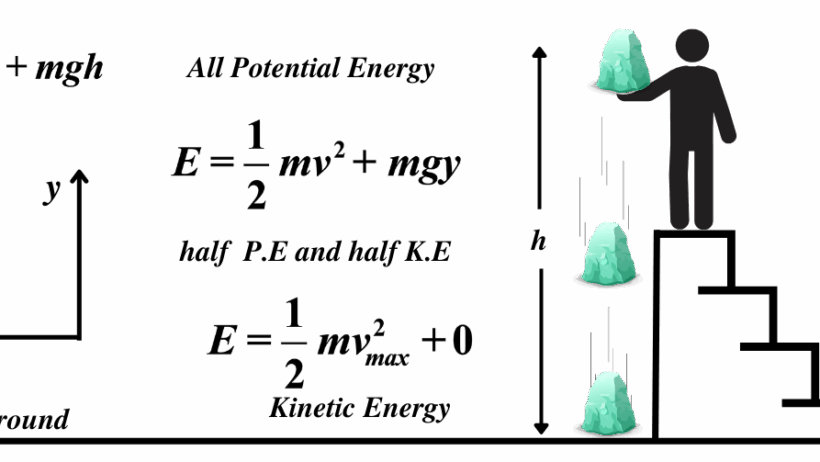
At its core, mechanical energy consists of two principal components—kinetic energy and potential energy. Kinetic energy relates to the motion of an object, quantified by the formula KE = 1/2 mv², where m represents mass and v denotes velocity. Potential energy, on the other hand, pertains to an object’s position relative to a gravitational field and can be articulated through the equation PE = mgh, with g being the acceleration due to gravity and h the height above a reference point. In the context of celestial mechanics, we often refer to gravitational potential energy, especially when considering large-scale bodies like the Earth and the Moon.
The Moon, with its orbital path around the Earth, exemplifies the principles of mechanical energy conservation beautifully. As the Moon orbits, it experiences continual changes in its velocity and position, which directly influence both its kinetic and potential energy. For instance, when the Moon is at perigee, the point in its orbit closest to Earth, its gravitational potential energy is at a minimum, while its kinetic energy is maximized due to the increase in orbital speed. Conversely, at apogee, the point farthest from Earth, the situation is reversed: potential energy reaches its zenith and kinetic energy diminishes.
Throughout its orbit, the total mechanical energy, which is the sum of the kinetic and potential energies, remains constant in the absence of external forces. This conservation law applies across countless systems within the universe, demonstrating the elegance of physical laws. Notably, the interplay of gravitational forces provides the necessary centripetal force that keeps the Moon in orbit. The Earth’s gravitational pull ensures that as the Moon accelerates towards Earth at perigee, it simultaneously retains its orbital path, adhering to Newton’s laws of motion.
The fascination with the Moon’s orbit extends beyond mere observation; it traverses the realms of historical, philosophical, and scientific inquiry. Ancient civilizations marveled at its regularity, attributing mystical significance to its phases. The Greek philosopher Aristotle postulated that celestial bodies moved in perfect circles, a view that persisted until advancements heralded by astronomers like Copernicus and Galileo. The intricate nature of the Moon’s orbit has sparked curiosity among scientists who endeavor to understand tidal forces, eclipses, and the very nature of gravitational interactions.
Consider tidal forces, a crucial consequence of the Moon’s gravitational influence on Earth. These forces not only exhibit the Moon’s capacity to affect large bodies of water but also serve as a tangible example of mechanical energy principles in action. The interaction between the Moon and Earth generates tides, which cyclically alter the potential energy of ocean waters as they rise and fall. This phenomenon illustrates how gravitational energy can manifest in observable ways that impact ecosystems and human activities alike.
Moreover, the Moon’s orbit is not a simple, circular path. Instead, it follows an elliptical shape, as described by Kepler’s laws of planetary motion. The first law states that the orbit of a planet is an ellipse with the sun at one focus, while the second law—often termed the law of equal areas—asserts that a line segment joining a planet and its star sweeps out equal areas during equal intervals of time. Consequently, as the Moon travels along its elliptical trajectory, it moves faster when closer to the Earth and slower when at a greater distance, reaffirming mechanical energy conservation throughout the orbit.
Further exploration into the interaction between the Moon and Earth reveals even more complexities. The presence of the Earth’s rotation and varying gravitational field modifies the straightforward conservation of mechanical energy. External influences, such as solar gravitational effects, can perturb the Moon’s orbit slightly. These perturbations manifest as changes in the Moon’s orbital parameters over time, which can be examined through meticulous calculations and observations.
Challenges in preserving our understanding of these celestial dynamics arise when examining the practical applications of the Moon’s orbit. The ancient practice of lunar calendars adapted to agricultural cycles illustrates the reliance of societies on the Moon’s predictable phases. In a modern context, the Moon’s position can be harnessed for navigational purposes in aviation and marine activities. Furthermore, ongoing research into the Moon’s gravitational potential provides insights into the feasibility of future lunar explorations and settlements, highlighting its significance within the broader framework of space exploration.
In conclusion, the Moon’s orbit is indeed a compelling example of mechanical energy conservation. The intricate dance between kinetic and potential energy, modulated by gravitational forces, encapsulates the elegance of physics governing celestial bodies. As we gaze up at our natural satellite, it serves as a constant reminder not only of the delicate balance within our solar system but also of the deeper interconnections that define our universe. The adventure of observing the Moon invites curiosity, exploration, and an appreciation for the natural laws that sustain both our planet and its lunar companion.