The interplay of mass, momentum, and energy forms a trio of fundamental principles in physics often referred to as the triple law of physics. These concepts, while distinct, are intricately connected and collectively govern the behavior of objects in motion, the transfer of energy, and the invariance of physical systems. Understanding these principles is paramount, especially in contexts such as engineering, environmental science, and mechanics. This discussion delves into the nuances of mass, momentum, and energy conservation, elucidating foundational concepts and their applications.
At the heart of this triad lies mass, a scalar quantity that reflects the amount of matter within an object. Mass is invariant; it does not change irrespective of the object’s location in the universe. It is instrumental in comprehending gravitational forces and inertial resistance. In classical mechanics, mass serves as a measure for determining how much force is necessary to alter an object’s state of motion. The unit of mass in the International System of Units (SI) is the kilogram (kg).
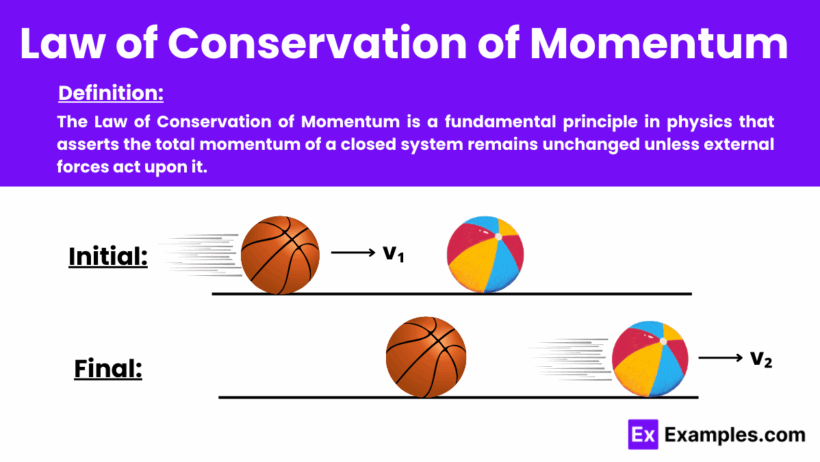
The concept of momentum is intrinsically linked to mass. Mathematically defined as the product of mass and velocity, momentum (p) can be expressed as p = mv, where ‘m’ denotes mass and ‘v’ represents velocity. This vector quantity not only provides insight into the motion of an object but also articulates the principle of conservation of momentum. According to this principle, in a closed system—absent external forces—the total momentum remains constant. Such a concept is indispensable in analyzing collisions and interactions among bodies, facilitating predictions about post-collision motion.
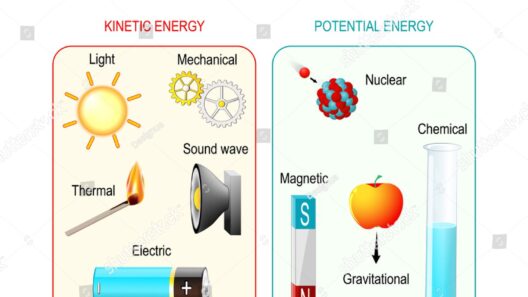
Energy, the third component of this tripartite framework, can be conceptualized in various forms: kinetic, potential, thermal, and more. The law of conservation of energy postulates that energy cannot be created or destroyed; it can only change from one form to another. This principle underpins a wide array of physical phenomena, from the mechanics of simple machines to the complexities of thermodynamics. Energy conservation dovetails with mass and momentum, particularly where energy transfers occur during interactions.
Connecting the Dots: To understand how mass, momentum, and energy conservation function cohesively, one must consider the implications of a system where these principles apply simultaneously. Take, for example, a closed system comprising two colliding objects. In such a scenario, the momentum before the collision can be calculated and will equal the momentum post-collision, provided there are no external forces acting upon it. Simultaneously, the total energy of the system, derived from kinetic and potential energy, must be conserved, confirming that energy simply transitions between forms during this interaction.
To explore these principles further, one can look at various types of collisions that elucidate the conservation of momentum and energy. Elastic collisions are instances where both momentum and kinetic energy are conserved. After the interaction, the objects rebound from one another, retaining their total kinetic energy. In contrast, an inelastic collision absorbs some kinetic energy, causing a transformation into other forms, such as heat, though momentum remains conserved. The distinction between these two types of collisions is crucial in fields such as crash analysis and material science.
Moreover, the concept of conservation of momentum extends beyond simple collisions and encompasses processes such as rocket propulsion. In this example, as fuel is expelled at high velocities in the opposite direction, the rocket experiences a forward thrust, demonstrating Newton’s third law of motion. The conservation of momentum ensures that the momentum gained by the rocket is equivalent to the momentum lost by the expelled mass. Here, mass, momentum, and energy are interwoven in a demonstration of their fundamental principles in action.
An exploration of energy in environmental contexts reveals the pressing importance of these principles in addressing contemporary challenges. The conservation of energy is particularly pertinent in discussions about renewable energy sources, where the objective is to harness energy from natural processes while minimizing waste. By understanding energy conservation, we can innovate technologies that sustain momentum towards a more energy-efficient future.
The implications of these principles extend to various fields. Engineers and physicists leverage the laws of momentum and energy in the design of structures, vehicles, and machinery, ensuring optimal performance while adhering to safety standards. Similarly, understanding conservation principles is critical in environmental science, where energy flow through ecosystems must be accounted for to assess the impact of human activities on biodiversity and resource sustainability.
In summary, the interrelationship of mass, momentum, and energy conservation forms an essential foundation for understanding the dynamics of physical systems. Through examining their connectedness, one gains a deeper appreciation of the forces that shape our world. The implications of these laws reach across multiple disciplines, fostering innovation and progress. As we seek to address pressing global challenges such as climate change and resource depletion, a grasp of these physics principles becomes increasingly vital. By embracing the power of these fundamental laws, society can transition towards a more sustainable future, where the conservation of our planet’s resources takes precedence.