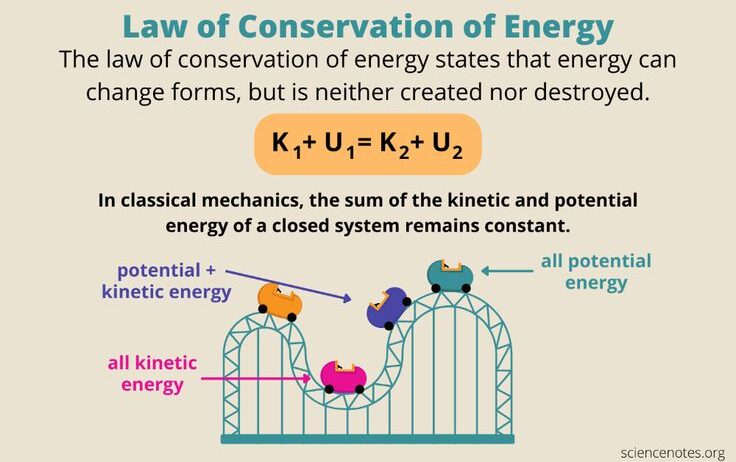
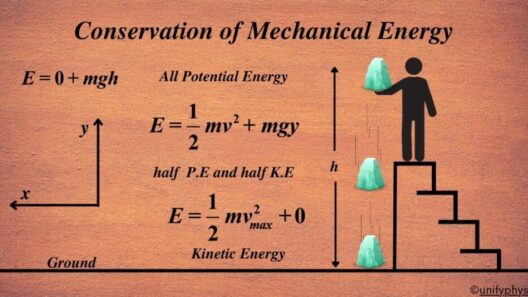
The Law of Conservation of Mechanical Energy is a fundamental principle in physics that asserts the total mechanical energy in a closed system remains constant if only conservative forces act on it. This principle is paramount not only in physics but also in various fields such as engineering, environmental science, and even economics, as it provides a framework for understanding how energy transforms and transfers between systems without loss. This article aims to elucidate the intricacies of this law, its mathematical formulation, and its practical implications.
To grasp the essence of mechanical energy, one must first delineate its two constitutive forms: kinetic energy and potential energy. Kinetic energy (KE) is the energy possessed by an object due to its motion, mathematically expressed as KE = 1/2 mv², where ‘m’ represents mass and ‘v’ signifies velocity. On the other hand, potential energy (PE) is the energy stored within an object due to its position or configuration, an archetype being gravitational potential energy, given by PE = mgh, with ‘g’ denoting the acceleration due to gravity and ‘h’ indicating height above the ground. The cumulative amount of kinetic and potential energy in a system delineates the machine’s mechanical energy.
The term “conservative forces” pertains to forces that do not dissipate energy as heat or other non-mechanical energies during interaction. Gravity is the quintessential example of a conservative force, as it performs work on objects without altering their total mechanical energy. A gripping illustration of this principle can be observed when a pendulum swings. At its highest point, the pendulum possesses maximum potential energy, which is then converted entirely into kinetic energy at the lowest point of its swing. In an idealized environment, where air resistance and friction are negligible, the energy constantly shifts between kinetic and potential forms, manifesting the law’s assertion that the total mechanical energy remains unchanged.
Mathematically, the Law of Conservation of Mechanical Energy can be succinctly encapsulated in the equation:
KE_initial + PE_initial = KE_final + PE_final
This equation underscores that the sum of kinetic and potential energy at any given point remains invariant. However, it warrants emphasis that this principle holds true only in isolated systems where no external work is done, and external forces do not intervene. Real-world applications often conjoin these theoretical principles with practical observations, unveiling complexities when non-conservative forces such as friction or air resistance come into play, thereby yielding a more nuanced understanding of mechanical energy transformations.
Consider a roller coaster as a practical demonstration of the Law of Conservation of Mechanical Energy: as the coaster ascends the highest points, it accumulates substantial potential energy. As it plummets downward, this potential is transmuted into kinetic energy, making the ride exhilarating. Herein lies a critical observation: while the total mechanical energy ideally remains constant, real-world factors — such as friction between the roller coaster and the tracks — result in energy losses primarily as thermal energy. This outcome showcases the importance of identifying conservative versus non-conservative forces in real-world applications.
Furthermore, the applications of the Law of Conservation of Mechanical Energy extend far beyond playground attractions. In various engineering disciplines, this principle underpins the design and analysis of mechanical systems, including vehicles, roller coasters, and wind turbines. The efficiency of such systems often relies on a comprehensive understanding of energy transformations, emphasizing the importance of minimizing energy losses to non-conservative forces. By recognizing how energy flows and transforms, engineers can devise solutions to enhance system performance.
Moreover, the conservation law is also pivotal in environmental discussions, particularly those around energy resources and sustainability. When analyzing energy consumption and resource allocation, acknowledging that energy cannot be created nor destroyed reinforces the need for sustainable practices. It compels society to focus on enhancing energy efficiency, developing renewable energy sources, and innovating ways to recycle energy within systems, thus conserving mechanical energy at a macro scale.
In educational settings, students are frequently introduced to this principle through hands-on experiments. One effective method involves using a simple pendulum or a cart on a track. Through observation and numerical calculations, students can witness the interplay between potential and kinetic energy, witnessing firsthand the elegant transition of energy forms while adhering to conservation laws. Such experiential learning reinforces theoretical grounding while promoting critical thinking skills.
In conclusion, the Law of Conservation of Mechanical Energy is an indispensable tenet that extends its reach into numerous facets of science and engineering. This principle not only enriches our understanding of physical phenomena but also encourages sustainable practices in our energy-centric world. Engaging with this law allows students to appreciate the interconnectedness of energy forms and the significance of conservation in a world where efficient resource management is critical for future viability. As such, a deep comprehension of mechanical energy conservation prepares students for the challenges that lie ahead, equipping them with the knowledge to innovate responsibly in various fields.