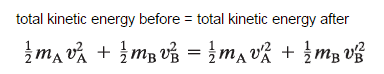Understanding the conservation of energy equation is pivotal in grasping how energy behaves within physical systems. This equation, often encapsulated in the form of E = mc², illustrates the profound relationship between mass and energy. To embark on this exploration, it is essential first to comprehend the foundational concepts inherent in energy conservation.
At its core, the principle of conservation of energy asserts that energy cannot be created or destroyed, only transformed from one form to another. This bedrock principle underpins countless phenomena in nature and technology. Its implications extend into various fields, including physics, engineering, and environmental science. By dissecting this equation, we unearth its significance and applications that promise a remarkable shift in our understanding of energy dynamics.
To delve deeper, let us outline the fundamental components of the conservation of energy equation. The equation itself typically takes several forms depending on the context, but ultimately converges on the same truth: total energy remains constant in an isolated system. The energy types involved are diverse, often categorized into kinetic, potential, thermal, and chemical energies, among others.
Kinetic energy, denoted by the formula ( KE = frac{1}{2}mv^2 ), is the energy possessed by an object due to its motion. Here, ( m ) represents the object’s mass and ( v ) symbolizes its velocity. Conversely, potential energy, expressed as ( PE = mgh ), reflects the energy stored within an object due to its position or state, where ( g ) is the gravitational constant and ( h ) signifies height. Understanding these components separately enriches one’s grasp of the conservation equation.
Next, we consider the total mechanical energy, which is the sum of the kinetic and potential energies in a closed system, represented mathematically as ( E_{total} = KE + PE ). This total remains constant, reinforcing the law of conservation. Physically, when one form of energy increases, another must correspondingly diminish, exemplifying the delicate balance within energy transactions. This relationship is not merely theoretical; it underlies the functioning of countless systems, from roller coasters to hydroelectric power plants.
Now, let’s apply these principles to real-world scenarios. Consider a roller coaster ascending a steep incline. As the coaster climbs, its speed decreases, and thus its kinetic energy diminishes. Simultaneously, as it gains altitude, potential energy accrues. When it crests the hill and begins to descend, the potential energy converts back into kinetic energy, propelling the coaster forward. Each moment of this journey echoes the conservation principle, illustrating the seamless interplay between energy forms.
Furthermore, this paradigm is not confined to mechanical systems. In thermodynamics, the conservation of energy principle manifests through the laws governing heat and work. In any thermodynamic process, the first law of thermodynamics states that the change in the internal energy of a system equates to the heat supplied to the system minus the work done by the system. This law profoundly influences applications in engineering, energy generation, and even room temperature. For instance, in designing efficient engines or power plants, the emphasis on minimizing energy loss during transformations becomes paramount.
As we transition to broader implications, the conservation of energy equation offers insights into sustainable practices and environmental stewardship. In a world increasingly conscious of climate change and resource depletion, understanding energy conservation transcends academic curiosity; it is imperative for mitigating ecological impacts. By harnessing renewable energy resources—such as solar, wind, and hydroelectric power—we embrace the potential to create energy without depleting natural reserves. Herein lies the promise of a sustainable future.
Moreover, the conservation equation lays a framework for encouraging energy efficiency in everyday life. Simple changes, such as utilizing energy-efficient appliances or practicing mindful consumption, contribute to the larger tapestry of energy conservation. When individuals recognize their contribution to the collective energy demand, they cultivate a sense of responsibility and agency. This shift in perspective creates a fascinating intersection between personal choices and global sustainability efforts.
In conclusion, understanding the conservation of energy equation opens avenues for curiosity and exploration. The interplay between kinetic and potential energy, the relevance of thermodynamics, and the environmental implications illuminates the profound significance of this principle. As we engage with this knowledge, we are empowered to affect change—personally and collectively. The call to action is clear: embrace a mindset geared towards energy conservation, not merely as an abstract concept but as an imperative for sustaining our planet and ensuring a resilient future.
Ultimately, the conservation of energy equation is more than a scientific formula; it is an invitation to rethink how we interact with our environment. With each small step towards energy conscious practices, we are not just participating in a discourse; we are contributing to a movement towards a sustainable and just world for future generations.