In the realm of physics, the exploration of energy transformation is not merely an academic exercise; it is a lens through which we can scrutinize fundamental principles of the universe. One such principle is the concept of mechanical energy, which is the sum of potential energy and kinetic energy in a system. The inquiry into whether mechanical energy was conserved in a falling mass experiment encapsulates profound insights into the nature of energy transfer, gravitation, and the laws governing motion.
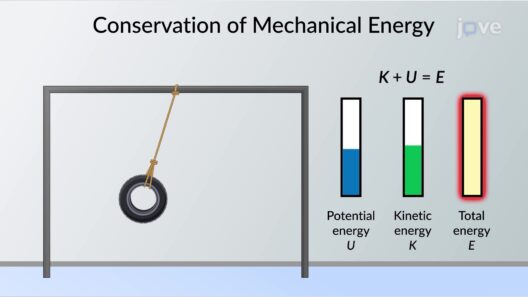
To comprehend this concept, one must first delve into the definitions of the two forms of mechanical energy. Potential energy is the stored energy possessed by an object due to its position or state, while kinetic energy is the energy of motion, dependent on an object’s mass and velocity. When evaluating a falling mass, such as a weight attached to a string or a rock released from a height, one observes a fascinating interaction between these two forms of energy.
As the mass is lifted and held at a height ( h ), it possesses gravitational potential energy, calculated using the equation ( PE = mgh ), where ( m ) represents mass, ( g ) is the acceleration due to gravity, and ( h ) is height. Upon release, the mass accelerates downward due to gravitational force, converting its potential energy into kinetic energy. As it descends, the kinetic energy increases, following the equation ( KE = frac{1}{2} mv^2 ), where ( v ) is the velocity of the mass.
But here arises a pivotal question: Is mechanical energy conserved throughout this process? The principle of conservation of mechanical energy stipulates that in an isolated system devoid of non-conservative forces, the total mechanical energy remains constant. In an ideal scenario, the potential energy at the apex of the fall would entirely convert into kinetic energy just before impact. Therefore, if the mass falls from a height ( h ), and assuming no other forces act upon it (like air resistance), the energy transformation would be seamless—an elegant dance of potential transitioning to kinetic energy.
However, the real-world environment complicates this theoretical simplicity. Although gravitational force acts relentlessly to draw the mass downward, frictional forces, air resistance, and other forms of energy dissipation come into play. When a mass falls through the atmosphere, it encounters air resistance, which can be categorized as a non-conservative force. This resistance acts contrary to the direction of motion, dissipating a portion of the mechanical energy as thermal energy due to friction between the object and air particles.
This introduction of air resistance raises an inquisitive dilemma: Does this external force nullify the conservation of mechanical energy in the falling mass experiment? The answer is nuanced. While total mechanical energy decreases—expressed as a loss of potential and kinetic energy due to energy dissipation—total energy within the system remains conserved. The loss in mechanical energy is matched by an equal gain in thermal energy. Thus, conservation is preserved when considering the broader realm of energy forms.
The implications of this understanding extend beyond theoretical physics; they prod at the very fabric of our societal energy practices. In an era marked by environmental challenges, acknowledging that not all energy transformations are ideal leads to a greater cognizance of efficiency in energy systems. Expertise in energy dissipation can inform strategies in technologies ranged from transportation to renewable energy sources. For instance, the design of wind turbines aims to optimize energy conversion while minimizing loss due to drag, ensuring that energy harnessed from nature translates into usable power effectively.
The inquiry into mechanical energy conservation fosters a wider perspective on energy consumption and ecological impact. A significant shift occurs when one begins to question not just the mechanical principles governing isolated systems, but also the broader implications of energy efficiency in everyday life. Energy conservation thus stands not merely as a matter of scientific intrigue, but as a clarion call for sustainable practices, urging society to embrace innovative approaches that transcend mere adherence to physical laws.
In the grand tapestry of environmental activism, understanding mechanical energy provides a bedrock for discussing issues like climate change, carbon footprints, and sustainable resource utilization. Each fragment of energy transformed during a falling mass experiment parallels the myriad energy exchanges in our ecosystems. Harnessing insights from these physical principles invites a reevaluation of traditional narratives surrounding energy application, yielding a proactive mindset geared towards resource stewardship.
In conclusion, the falling mass experiment not only illuminates the principles of mechanical energy conservation but also instigates curiosity about the interplay of energy forms in our world. The conceptual journey from potential energy at rest to kinetic energy in motion serves as a metaphor for our potential to enact change in energy use—tangibly manifesting our understanding of energy conservation into actionable practices. As we navigate the complexities of the present and future energy landscape, let us foster a conscious dialogue around energy efficiency and sustainability, spurred on by fundamental scientific principles that govern motion and energy in both isolated and interconnected systems.