Conservation of mechanical energy is a pivotal concept in physics, encapsulating the intricate relationship between kinetic and potential energy within a closed system. This principle states that in the absence of non-conservative forces, such as friction or air resistance, the total mechanical energy of an object remains constant. It is a captivating notion, fundamentally connecting various phenomena observed in the physical world, from the mundane act of a ball rolling down a hill to the grand complexities of planetary motion.
To unpack the essence of this principle, one must first grasp the definitions of kinetic and potential energy. Kinetic energy is the energy possessed by an object due to its motion, determined by the formula K.E. = (1/2)mv², where m signifies mass and v denotes velocity. Conversely, potential energy is the energy stored in an object based on its position or configuration, typically exemplified by gravitational potential energy calculated as P.E. = mgh, where h represents height. These forms of energy are not isolated from one another; rather, they are interdependent facets of mechanical energy that exhibit an exquisite balance throughout physical processes.
One of the most relatable illustrations of conservation of mechanical energy is a simple pendulum. As the pendulum swings, it oscillates between its maximum height—where its potential energy is at its zenith—and the lowest point—where its kinetic energy reaches its peak. At the apex of its swing, the pendulum has converted all of its kinetic energy into potential energy. As it descends, potential energy diminishes while kinetic energy ascends, preserving the total mechanical energy throughout the motion. This cyclical transformation between energy types embodies the principles of conservation, demonstrating a perpetual dance of creation and annihilation, devoid of external influence.
In practical applications, understanding mechanical energy conservation is vital across diverse fields ranging from engineering to environmental science. Hydroelectric power generation, for instance, showcases a practical implementation of this principle. The potential energy of water stored in a dam is transformed into kinetic energy as it flows downward to turn turbines, subsequently generating electrical energy. This transformation underscores the efficiency of harnessing nature’s energy while minimizing waste, promoting sustainability within energy practices.
Another fascinating dimension of conservation of mechanical energy lies in the context of celestial mechanics. The motion of planets around the sun can be elucidated through this principle. As planets orbit, they interplay between potential energy—due to their position relative to the sun—and kinetic energy—as they travel along their elliptical trajectories. The conservation of mechanical energy fundamentally governs their motion, allowing us to predict celestial events with remarkable accuracy.
Within the realm of sports and biomechanics, the conservation of mechanical energy offers insights into optimizing human performance. Athletes utilize the principles of energy conservation to enhance their efficiency. For instance, rhythmic movements in running or swimming facilitate energy transfer, allowing athletes to maintain speed without expending excess energy. Understanding these dynamics can lead to improved training methods, enhancing performance while minimizing injury risk.
Despite its apparent simplicity, the implications of conservation of mechanical energy resonate deeply in both academic and real-world contexts. It compels us to question our interaction with the environment and fosters a deeper appreciation for the flows of energy present in nature. The intricate balance of forces, energy exchanges, and systemic behaviors encapsulated within this principle culminates in an awe-inspiring journey of discovery.
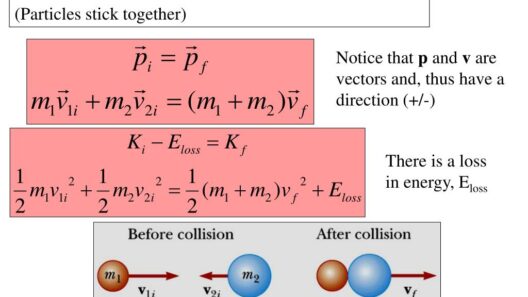
Moreover, the principle transcends mere mechanics; it forms a cornerstone of our understanding of various physical phenomena. For instance, conservation laws often draw a parallel with other fundamental conservation principles, such as conservation of momentum. Two colliding objects demonstrate both momentum and mechanical energy conservation, offering a comprehensive framework for analyzing collisions in particle physics or vehicular dynamics. These interconnections exemplify the beauty of physics as an interconnected holistic discipline, where one principle illuminates the nuances of others.
Real-life observations also reveal that the conservation of mechanical energy extends to natural systems. The processes of ecosystems, from the energy captured through photosynthesis to its release during respiration, echo this principle. The energy in food, derived ultimately from sunlight, moves through trophic levels, adhering to the conservation of energy schemes, manifesting the elegance of energy flow and transformation in the biosphere.
As society aims for greater sustainability and energy efficiency, the profound understanding of mechanical energy conservation holds significant promise. It drives innovations in renewable technologies and energy storage solutions, promoting a shift towards harmonious living with our environment. By embracing these principles, we pave the way for a future where energy is utilized more wisely, fostering ecological balance and reducing our carbon footprint.
In conclusion, the conservation of mechanical energy is not merely a physics principle confined to textbooks; it is the very fabric that wields influence over myriad aspects of our world. The interplay between kinetic and potential energy paints a vivid picture of the natural laws at play in our environment. By delving into these principles, we not only gain insight into fundamental physics but also appreciate the intricate connections between energy, motion, and existence. It invites us to explore, question, and innovate within the vast landscape of energy conservation, inspiring a commitment to stewardship of our planet for generations to come.