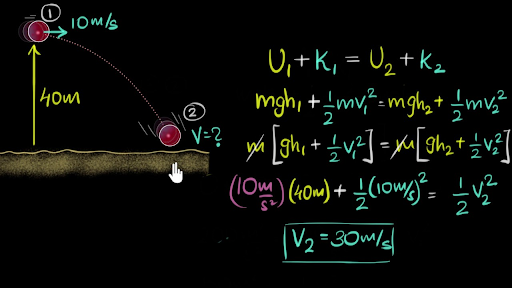
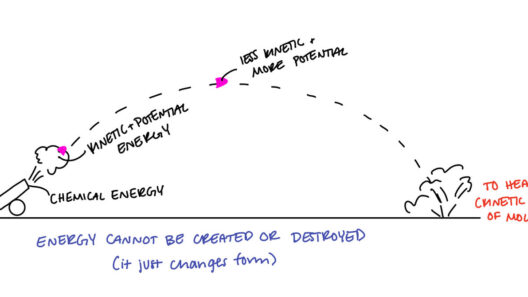
The Law of Conservation of Energy is a fundamental principle in physics that articulates a vital observation in our universe: the total energy of an isolated system remains constant over time. This concept is not just a cornerstone of physics; it resonates deeply within various scientific disciplines, from thermodynamics to quantum mechanics. This law serves as a reminder of the intricate balance that governs our world, where energy is neither created nor destroyed but rather transformed from one form to another. At the heart of this law lies a remarkable equation that elegantly encapsulates this principle: the equation of energy conservation.
Mathematically, the Law of Conservation of Energy can be expressed as:
E_initial = E_final
Or, in a more detailed expression involving various forms of energy, it can be presented as:
KE_initial + PE_initial + sum E_{other_initial} = KE_final + PE_final + sum E_{other_final}
Where KE represents kinetic energy, PE signifies potential energy, and E_other encompasses all other forms of energy, such as thermal, chemical, and electrical energy. This equation underscores that the sum of all forms of energy in a closed system remains invariant, regardless of the processes occurring within it.
Energy exists in numerous forms. Kinetic energy (KE), for instance, is associated with the motion of an object and can be quantified by the equation:
KE = frac{1}{2}mv^2
In this equation, m denotes the mass of the object, while v represents its velocity. Conversely, potential energy (PE) is related to an object’s position within a force field, such as gravitational or elastic fields. The classical expression for gravitational potential energy is:
PE = mgh
In this scenario, g stands for the acceleration due to gravity, and h designates the height above a reference point. This transformation between kinetic and potential forms of energy becomes evident in scenarios like a pendulum’s swing—where energy constantly shifts between kinetic and potential states while the total energy remains conserved.
The fascination with the Law of Conservation of Energy lies not only in its mathematical representation but also in its far-reaching implications. One of the most profound examples is seen in the context of ecosystems. Here, energy flows from the sun to plants through photosynthesis, subsequently transferring to herbivores and further up the food chain. This energy transfer intricately weaves life together, revealing the interconnectedness of all living organisms. Each transition embodies the essence of energy transformation while adhering to the law’s fundamental framework.
Moreover, the conservation of energy principle is critical in understanding our role in combating climate change. In everyday life, energy is transformed from one form to another through various processes, such as combustion in vehicles or electrical generation in power plants. In these systems, understanding and optimizing the energy transfer processes can significantly mitigate our carbon footprint. Emphasizing renewable energy sources—such as solar, wind, and hydroelectric power—especially underscores the urgency of transitioning toward sustainable energy practices.
In the broader context, engineers and scientists utilize the Law of Conservation of Energy to design more efficient systems. An example is the development of heat engines, which convert thermal energy into work. The efficiency of these engines can be evaluated via the first law of thermodynamics, a principle derived from the conservation of energy. This relationship illustrates how critical energy conservation is in engineering applications and technology development.
Additionally, modern physics expands upon classical mechanical principles, highlighting the significance of energy conservation in quantum mechanics. Here, the notion achieves a subtle and captivating dimension, where energy conservation is observed even at the minutest scales. The conservation laws integrate seamlessly with the framework of quantum field theory, underscoring the universality of energy conservation across all levels of reality.
The philosophical implications of the conservation of energy are equally compelling. It poses intriguing questions about the nature of existence and the universe. If energy can never truly be lost, what does that imply about life, death, and rebirth? This contemplation invites perspectives that transcend mere scientific inquiry, engaging with metaphysical discussions about the cycle of life, the continuity of energy, and the essence of change.
The universality of the Law of Conservation of Energy is a powerful lens through which we can view interactions in both natural and engineered systems. In a world increasingly dependent on technology, energy conservation remains a priority, underscoring our responsibility to harness energy wisely and sustainably. By focusing on energy efficiency and renewable resources, we can ensure that future generations inherit a planet where the balance of energy within ecosystems and human constructs persists.
In conclusion, the Law of Conservation of Energy encapsulates a fundamental truth that governs the universe. Its mathematical representation embodies both simplicity and profundity, resonating through myriad applications, whether in nature, technology, or philosophy. As we continue to grapple with complex global challenges, the principles inherent in energy conservation will guide our path toward a sustainable future and emphasize the vital interconnectedness of all existence.