Mechanical energy, in its essence, is the sum of kinetic and potential energy within an object that is in motion or under the influence of a gravitational field. The conservation of mechanical energy is a fundamental principle in physics, encapsulating the notion that in an isolated system with no external forces, the total mechanical energy remains constant over time. This principle serves as a critical foundation for understanding various phenomena in both classical mechanics and various real-world applications.
To delve deeper into the concept, it is essential to distinguish between two forms of mechanical energy: kinetic energy and potential energy. Kinetic energy is the energy of an object due to its motion, expressed mathematically as K.E. = 1/2 mv², where m represents mass and v represents velocity. As an object’s speed increases, its kinetic energy amplifies exponentially due to the square dependence on velocity.
On the other hand, potential energy refers to the stored energy of an object due to its position or configuration. Gravitational potential energy, for instance, is calculated by the formula P.E. = mgh, where g is the acceleration due to gravity and h is the height above a reference point. The interplay between these energies becomes particularly fascinating when considering systems where energy is conserved, leading to intriguing behaviors that defy intuitive understanding.
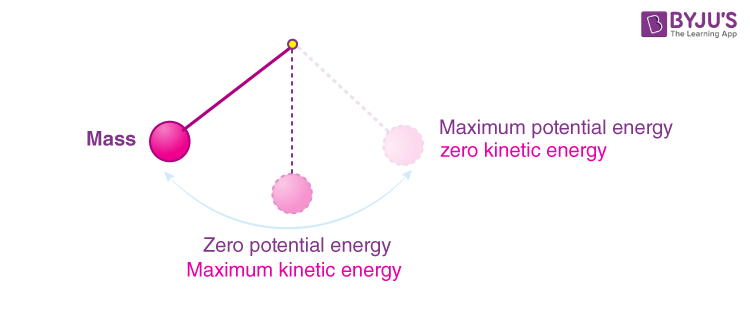
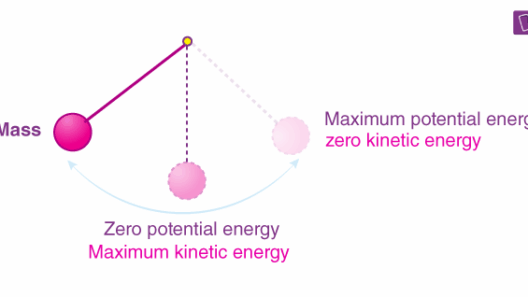
In a closed system devoid of external forces, as an object transitions between kinetic and potential energy, the first law of thermodynamics kicks in, affirming that the total mechanical energy remains a constant value. This conservation principle can be observed in various scenarios, such as the motion of a pendulum. At its highest point, the pendulum possesses maximal potential energy and minimal kinetic energy. As it swings downward, potential energy is converted into kinetic energy, reaching its apex of speed at the lowest point in its trajectory. When the pendulum ascends again, kinetic energy wanes as potential energy accumulates, illustrating the seamless exchange between these energy forms while maintaining a constant total amount.
Moreover, the conservation of mechanical energy is not merely a theoretical construct but has practical implications within numerous fields such as engineering, astrophysics, and environmental science. For instance, roller coasters are engineered using principles of conservation of energy. As the coaster climbs to a peak, energy is stored as potential energy. Upon descending, this potential energy is converted into kinetic energy, powering the thrilling experience while minimizing the need for additional energy input.
One may also observe the conservation of mechanical energy in natural systems. Consider a waterfall: as water cascades down, it transitions from potential energy at its height to kinetic energy in descent, transferring vast amounts of energy to its surroundings and potentially even generating electricity through hydropower. Such ecosystems demonstrate the cyclical flow of energy, reaffirming the relentless and intricate balance of nature’s mechanics.
It’s crucial to recognize, however, that conservation of mechanical energy holds true only in ideal conditions, devoid of losses from external forces such as friction, air resistance, or any other dissipative forces. In real-world applications, non-conservative forces can cause energy to dissipate, leading to a decrease in total mechanical energy. This rectitude is evident in the operation of mechanical systems: gears and motors experience friction, requiring additional energy input to maintain functionality. Thus, while the conservation of mechanical energy principle remains a vital component of physics, it is often necessary to account for real-world imperfections when conducting analyses.
The implications of understanding mechanical energy conservation extend beyond academic curiosity; they also foster a deeper appreciation for sustainability. As societies globally face the pressing challenge of resource depletion and climate change, harnessing knowledge about energy conservation can lead to innovative practices that mitigate environmental impact. Solutions such as energy-efficient designs and renewable energy technologies can be informed by principles of mechanical energy conservation, allowing for the development of sustainable systems that minimize energy waste and maximize efficiency.
Additionally, the educational aspect of energy conservation is vital. By instilling a foundation in physics principles among students, we can steer budding thinkers towards a more profound respect and understanding of energy resources. This comprehension may inspire future generations to pursue advancements in technology and innovation that prioritize sustainable energy solution.
In retrospection, the fascination with conserved mechanical energy lies not merely in its mathematical representations, but rather in its capacity to explain and predict the behavior of countless objects and systems, from the ordinary swing of a pendulum to the majestic arcs of celestial bodies. It denotes a universal constant in our physical world, threading through various phenomena and bridging diverse fields of study. Moreover, it serves as a testament to the intricate interrelations between motion, energy, and nature. In conclusion, acknowledging the principles of mechanical energy conservation not only enriches our understanding of physical sciences but also bolsters the imperative for energy mindfulness in the contemporary world.