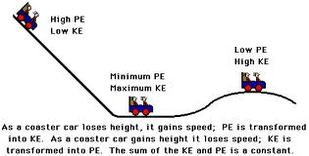
Kinetic energy, the energy possessed by an object due to its motion, is a fundamental concept in physics that lays the groundwork for understanding various phenomena—from car crashes to sports dynamics. However, the question remains: when is kinetic energy conserved? Comprehending the circumstances that allow kinetic energy to remain constant is crucial in multiple fields, including engineering, mechanics, and even environmental science.
Understanding the principles of conservation of energy will lead to a deeper appreciation of kinetic energy. Conservation of energy states that in a closed system, the total energy remains constant over time. While this principle applies universally, the specific conditions under which kinetic energy is conserved require further investigation.
The following exploration will elucidate the concept of kinetic energy, its conservation, and the circumstances that influence its behavior during elastic and inelastic collisions.
Defining Kinetic Energy
Kinetic energy can be expressed mathematically as KE = ½ mv², where ‘m’ represents mass and ‘v’ denotes velocity. This simple yet powerful equation reveals that an increase in either the mass of an object or its velocity will result in a proportional increase in kinetic energy. Nonetheless, it’s essential to understand that kinetic energy is a scalar quantity, meaning it has magnitude but no directional attributes. Thus, it is crucial to distinguish kinetic energy from vector quantities like momentum, which encompass both magnitude and direction.
Crucial to a comprehensive understanding of kinetic energy is the stipulation that it’s not always conserved. In fact, the conservation of kinetic energy only happens under certain conditions. These nuances merit profound examination as they reveal the complexities of motion and energy transfer.
Elastic Collisions: A Case of Conservation
Elastic collisions represent one of the most riveting phenomena regarding the conservation of kinetic energy. In an ideal elastic collision, both momentum and kinetic energy are conserved. This means that when two objects collide and bounce apart without any deformation or generation of heat, the total kinetic energy before and after the collision remains unchanged. Common examples include collisions between billiard balls or molecules in a gas.
A detailed breakdown of elastic collisions reveals their mechanics. When two elastic bodies collide head-on, the kinetic energy transfers between them while the sum remains constant. This transfer is consumingly fascinating; the velocities of the objects often change, yet the overall kinetic energy remains intact, showcasing the beauty of energy routing through momentum while abiding by the law of conservation.
Inelastic Collisions: The Paradigm Shift
Conversely, inelastic collisions present a contrasting scenario where kinetic energy is not conserved during the interaction. While momentum remains constant in a closed system, kinetic energy is transformed into other forms, such as heat, sound, or deformation. A common illustration of an inelastic collision can be observed in a car crash—the total kinetic energy before impact exceeds that after the objects entangle, dissipating energy through crumpling metal and the sound of collision.
Understanding the mechanics of inelastic collisions is critical in fields like automobile safety engineering. Crash test simulations help engineers design vehicles that mitigate energy transfer during accidents, illustrating the application of kinetic energy principles in real-world situations. By utilizing the energy absorption capabilities of materials, safety innovations continue to evolve, pushing the boundaries of passenger safety.
Factors Influencing Kinetic Energy Conservation
To delve deeper into when kinetic energy remains unchanged, several crucial factors must be weighed. Primarily, the nature of the collision dictates whether kinetic energy will be preserved: elastic versus inelastic. Additionally, external forces play a foundational role. When external forces act on a system—such as friction or air resistance—energy is diverted from kinetic energy to other forms, causing it to dissipate. These forces alter the energy landscape of an object, illustrating the importance of recognizing the environment in which energy conservation laws apply.
Another significant factor is the existence of isolated systems. In physics, a system isolated from external forces ensures that the principles of conservation apply unimpeded. The presence of external interactions invariably leads to energy loss, affecting the conservation of kinetic energy. For practical applications, achieving an isolated condition can be nearly impossible, yet it’s a vital consideration for theoretical analyses.
Conclusion: Embracing the Complexity of Kinetic Energy Conservation
In summary, the conservation of kinetic energy is a fascinating interplay of physics that not only enriches our understanding of motion but also informs practical applications in safety, engineering, and science. Through the lens of elastic and inelastic collisions, one can appreciate how energy transforms and redistributes, yet remains bound by conservation laws. Considering various factors such as external forces and system isolation uncovers the complexities of kinetic energy conservation and its real-world ramifications.
Ultimately, grasping when kinetic energy is conserved helps clarify fundamental principles that govern both natural and engineered systems. As we continue exploring the boundaries of knowledge in physics, the intricacies of energy conservation remain a testament to the elegance and profundity of the universe. Understanding these principles will allow not only for advancements in technology but also foster a more profound appreciation of the forces that shape our world.